任意 n 阶段矩阵 M 可以看成由 n 个列向量 c1 c2 ... cn 组成:
M=[c1c2...cn]
将这 n 个列向量进行线性变换后所能表示的向量记为 v 有:
v=k1c1+k2c2+...+kncn
所有 v 构成的向量空间记为 R
相关信息
表示由矩阵的列向量所能构成的向量所组成的向量空间 R 的维度
表示该矩阵对空间进行变换的缩放程度,例如,2 阶矩阵表示面积的缩放,3 阶矩阵表示体积的缩放 如果行列式为 0,表示该矩阵变换进行了降维操作(即秩⬇),因此此时矩阵不可逆 如果行列式 < 0,表示该矩阵变换进行了翻转操作
线性变换定义
f(x)+f(y)kf(x)=f(x+y)=f(kx)
对于任意矩阵 M 以及向量 x y 满足:
Mx + My = M(x+y)
kM(x) = M(kx)
因此 M 也满足线性变换
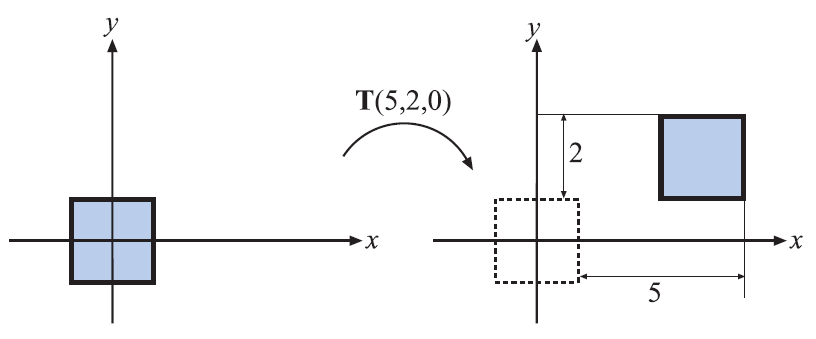
T(t)=T(tx,ty,tz)=100001000010txtytz1
Rx(ϕ)=10000cosϕsinϕ00−sinϕcosϕ00001
Ry(ϕ)=cosϕ0−sinϕ00100sinϕ0cosϕ00001
Rz(ϕ)=cosϕsinϕ00−sinϕcosϕ0000100001
定理
任意 3x3 旋转矩阵都是标准正交矩阵,且行列式等于 1
给定由一组标准正交基所组成的矩阵 A 以及任意 3x3 旋转矩阵 R,其旋转之后仍然是一组标准正交基,可得:
(RA)(RA)T=RAATRT=RRT=I
S(s)=sx0000sy0000sz00001
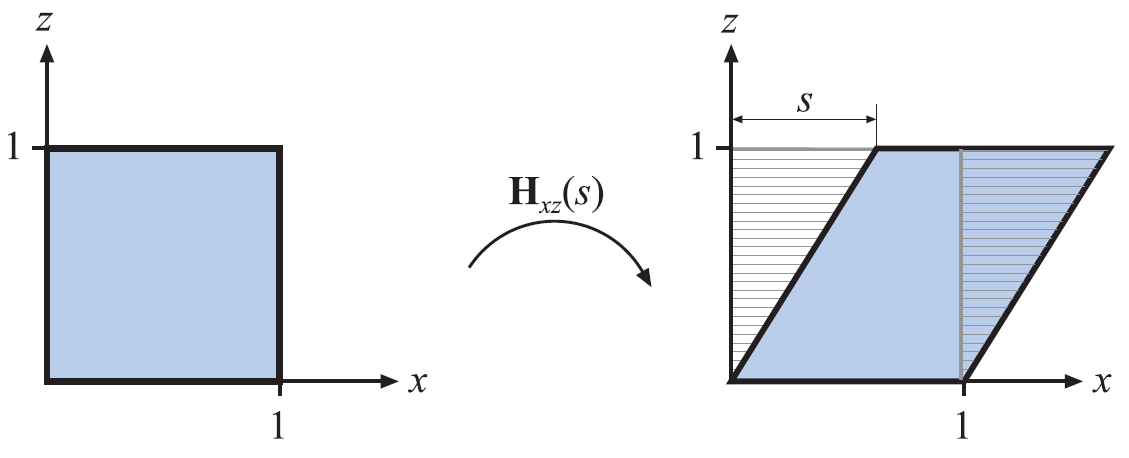
Hxz(s)=10000100s0100001
记 n 和 t 为变换前的法线和切线,n' 和 t' 为变换后的法线和切线,M 为顶点变换矩阵,S 为法线变换矩阵
n′Tt′=(Sn)T(Mt)=nTSTMt=0=nTt
则
STM=I⇒S=(M−1)T
当 M 只包含旋转和统一缩放变换时,S = M
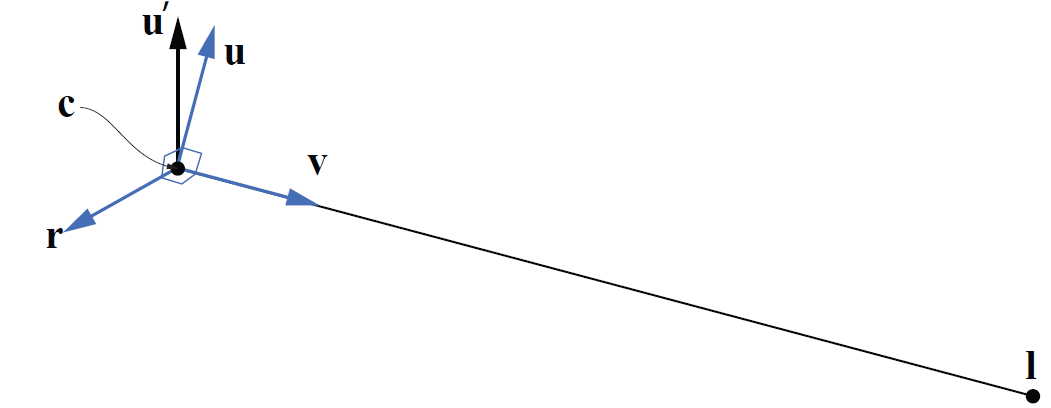
如图,假定相机位置在 c,单位向量 r,u,v 表示相机的旋转朝向
提示
由于相机和物体之间的相对位置是固定不变的,我们可以先对整体一起进行矩阵变换,使得相机位于原点且朝向从 <r,u,v> 变换为 <x,y,z> (当然也可以变换为 x,y,-z)
- 先将相机平移到原点
Tview=100001000010−tx−ty−tz1
- 将朝向从 <r,u,v> 变换为 <x,y,z>
提示
可以单独考虑每个向量,我们希望通过一个旋转矩阵变换将 r → x(<1,0,0>), u → y(<0,1,0>), v → z(<0,0,1>),因为 r,u,v 是标准正交向量,所以 r·r = u·u = v·v = 1,且两两之间的点积为 0
综上,可以推导出对应的旋转矩阵
Rview=rTuTvT00001=rxuxvx0ryuyvy0rzuzvz00001
- 视图变换矩阵
Mview=RviewTview=rxuxvx0ryuyvy0rzuzvz00001100001000010−tx−ty−tz1=rxuxvx0ryuyvy0rzuzvz0−t⋅r−t⋅u−t⋅v1
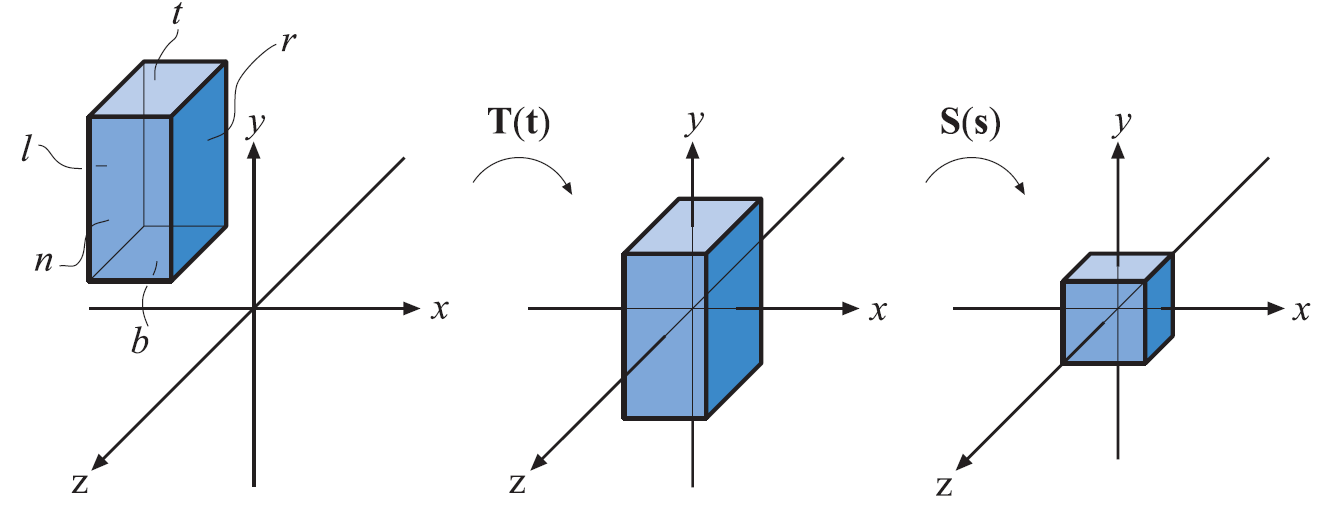
提示
正交投影的目标是将由(l,r,b,t,n,f)所表示的 AABB 变换到以原点为中心的标准 AABB,在 OpenGL 中标准 AABB 为 (-1,-1,-1) - (1,1,1),在 DirectX 中标准 AABB 为 (-1,-1,0) - (1,1,1)
注意
上图中相机看向 -z 的方向,因此有 0 > n > f; 如果相机看向 +z 的方向,那么 0 < n < f,并且投影矩阵公式也会有所不同,以下公式推导基于相机看向 +z 方向
Po[−1,1]=S(s)T(t)=r−l20000t−b20000f−n200001100001000010−2l+r−2b+t−2n+f1=r−l20000t−b20000f−n20l−rl+rb−tb+tn−fn+f1
Po[0,1]=MstPo[−1,1]=10000100000.50000.51r−l20000t−b20000f−n20l−rl+rb−tb+tn−fn+f1=r−l20000t−b20000f−n10l−rl+rb−tb+tn−fn1
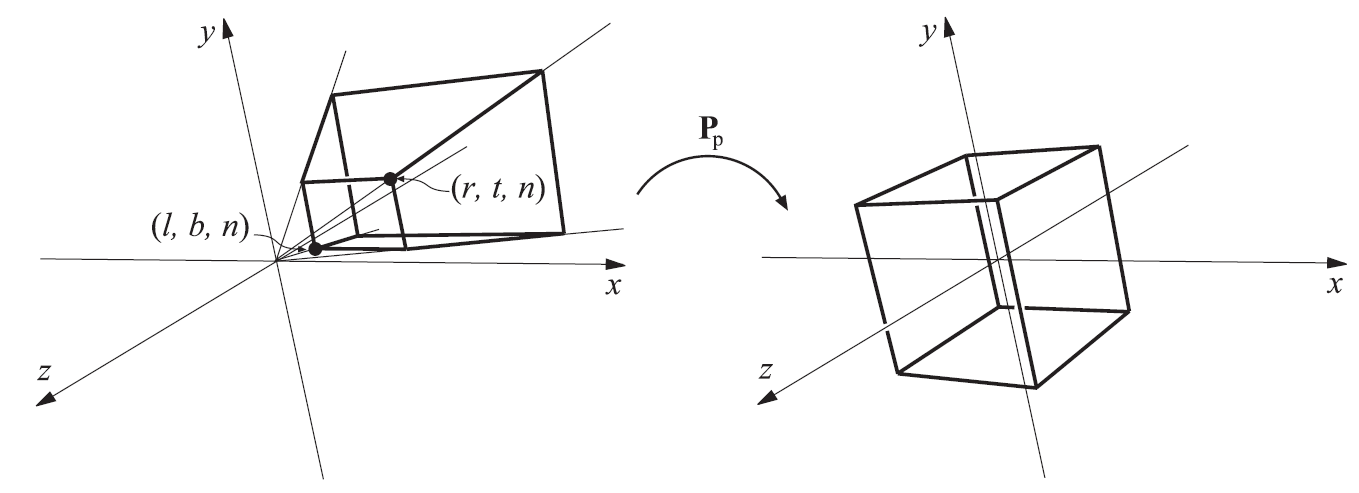
提示
透视投影的目标是将由(l,r,b,t,n,f)所表示的视锥体变换到以原点为中心的标准 AABB,在 OpenGL 中标准 AABB 为 (-1,-1,-1) - (1,1,1),在 DirectX 中标准 AABB 为 (-1,-1,0) - (1,1,1)
注意
上图中相机看向 -z 的方向,因此有 0 > n > f; 如果相机看向 +z 的方向,那么 0 < n < f,并且投影矩阵公式也会有所不同,以下公式推导基于相机看向 +z 方向
直接计算这个变化有困难,可以考虑分成两步
第一步
将由(l,r,b,t,n,f)所表示的视锥体变换到由(l,r,b,t,n,f)所表示的 AABB,即把视锥体往中间压缩成一个长方体,且保持近平面和远平面的距离不变
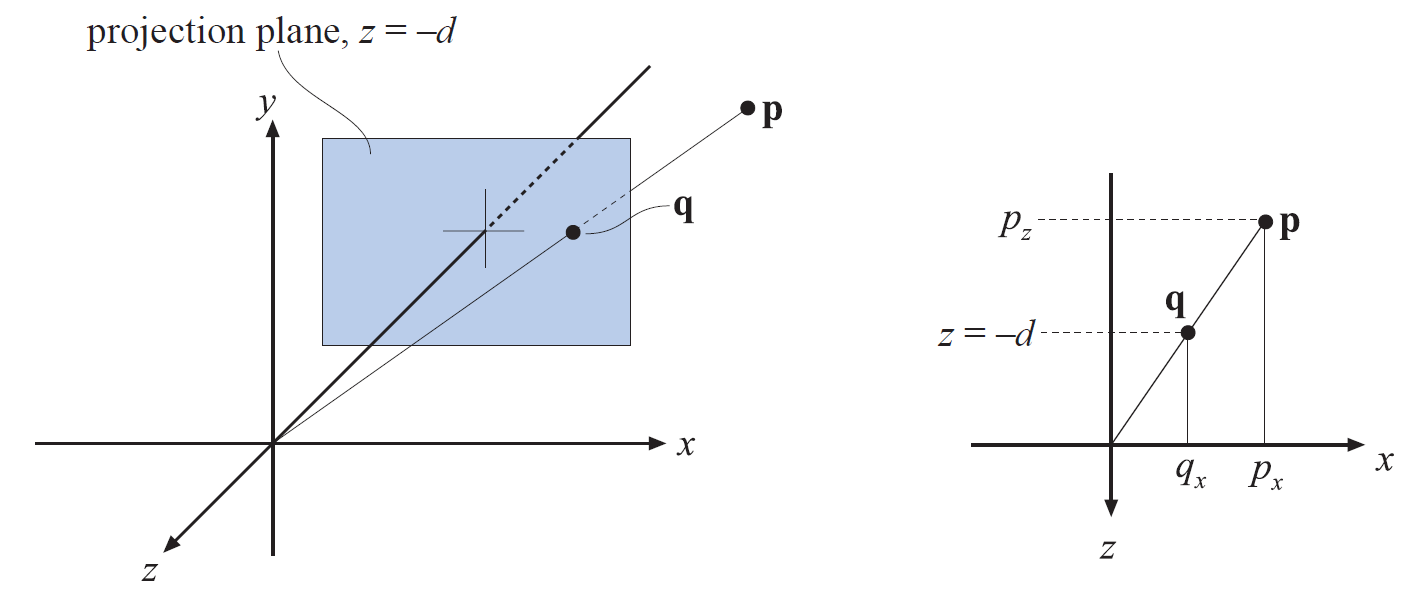 i. 推导矩阵信息
i. 推导矩阵信息任意点 p(x, y, z) 投影到近平面上的位置为 q(nx/z, ny/z, n),我们取 qx 和 qy 作为压缩后的 x 和 y,而压缩之后的 z 暂且不管,即我们要求一个矩阵变换,使得:
xyz1⇒nx/zny/z?1==nxny?z
据此,可以推导出该矩阵的一部分信息
Mpersp→ortho=n0?00n?000?100?0
ii. 计算矩阵第三行元素我们可以知道,在近平面和远平面上的点,经过压缩变换之后 z 坐标的值保持不变,即
xyn1⇒xyn1==nxnyn2n
xyf1⇒xyf1==fxfyf2f
其中 x, y 是变量,而 n 是常量和 x, y 无关,因此矩阵第三行一定是 (0 0 A B) 的形式,因此有
An+B=n2Af+B=f2⇒AB=n+f=−nf
综上
Mpersp→ortho=n0000n0000n+f100−nf0
第二步
将由(l,r,b,t,n,f)所表示的 AABB 变换到以原点为中心的标准 AABB,在 OpenGL 中标准 AABB 为 (-1,-1,-1) - (1,1,1),在 DirectX 中标准 AABB 为 (-1,-1,0) - (1,1,1)
这一步其实就是前面正交投影变换的过程!
Mortho=r−l20000t−b20000f−n20l−rl+rb−tb+tn−fn+f1
Mortho=r−l20000t−b20000f−n10l−rl+rb−tb+tn−fn1
第三步
P=Mortho⋅Mpersp→ortho
Pp[−1,1]=Mortho⋅Mpersp→ortho=r−l20000t−b20000f−n20l−rl+rb−tb+tn−fn+f1n0000n0000n+f100−nf0=r−l2n0000t−b2n00l−rl+rb−tb+t−n−fn+f100n−f2nf0
Pp[0,1]=Mortho⋅Mpersp→ortho=r−l20000t−b20000f−n10l−rl+rb−tb+tn−fn1n0000n0000n+f100−nf0=r−l2n0000t−b2n00l−rl+rb−tb+t−n−ff100n−fnf0
相关信息
经过投影变换后,从相机坐标空间转换为 NDC 坐标空间
提示
视口变换的目标是将 xy 坐标从 [-1, 1] x [-1, 1] 变换到 [0, width] x [0, height],z 坐标保持不变
Mviewport=2width00002height0000102width2height01





