分治

矩阵相乘

matrix_multiply(A,B,C,n)
  for i = 1 to n
    for j = 1 to n
      for k = 1 to n
        C[i][j] = C[i][j] + A[i][k] * B[k][j]

时间复杂度为 $\Theta(n^3)$

矩阵相乘（分治）

$$\begin{aligned} \begin{pmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{pmatrix} &= \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix} \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix} \\[6pt] &= \begin{pmatrix} A_{11}\cdot B_{11}+A_{12}\cdot B_{21} & A_{11}\cdot B_{12}+A_{12}\cdot B_{22} \\ A_{21}\cdot B_{11}+A_{22}\cdot B_{21} & A_{21}\cdot B_{12}+A_{22}\cdot B_{22} \end{pmatrix} \end{aligned}$$

matrix_multiply_recursive(A,B,C,n)
  if n == 1
    // Base case.
    C[1][1] = C[1][1] + A[1][1] * B[1][1]
    return
  // Divide.
  partition A,B,and C into n/2 x n/2 submatrices
  // Conquer.
  matrix_multiply_recursive(A₁₁,B₁₁,C₁₁,n/2)
  matrix_multiply_recursive(A₁₁,B₁₂,C₁₂,n/2)
  matrix_multiply_recursive(A₂₁,B₁₁,C₂₁,n/2)
  matrix_multiply_recursive(A₂₁,B₁₂,C₂₂,n/2)
  matrix_multiply_recursive(A₁₂,B₂₁,C₁₁,n/2)
  matrix_multiply_recursive(A₁₂,B₂₂,C₁₂,n/2)
  matrix_multiply_recursive(A₂₂,B₂₁,C₂₁,n/2)
  matrix_multiply_recursive(A₂₂,B₂₂,C₂₂,n/2)

时间复杂度为

$$T(n) = 8T(n/2) + \Theta(1) = \Theta(n^3)$$

矩阵相乘（Strassen）

提示

基本思想是将子问题从8次矩阵乘法减少到7次，代价是4次矩阵加法增加到18次，从而降低了总的时间复杂度

时间复杂度为

$$T(n) = 7T(n/2) + \Theta(n^2) = \Theta(n^{lg7}) = O(n^{2.81})$$

递归时间复杂度计算方法

替换法

提示

替换法主要分为两个步骤：1. 猜测 2. 使用数学归纳法进行证明

下面我们使用替换法来计算以下这个递归的时间复杂度

$$T(n)=2T(\lfloor n/2 \rfloor)+\Theta(n)$$

1. 猜测

$$T(n)=\mathcal{O}(nlgn)$$

2. 证明
   当 n >= 2n₀ 时有

$$\begin{aligned} T(n) &\le 2c\lfloor n/2 \rfloor lg(\lfloor n/2 \rfloor) + \Theta(n) \\[6pt] &\le 2c(n/2)lg(n/2)+\Theta(n) \\[6pt] &= cnlg(n/2)+\Theta(n) \\[6pt] &= cnlgn - cn+\Theta(n) \\[6pt] &\le cnlgn \end{aligned}$$

只要 c 取得足够大，就能保证最后的不等式成立

递归树法

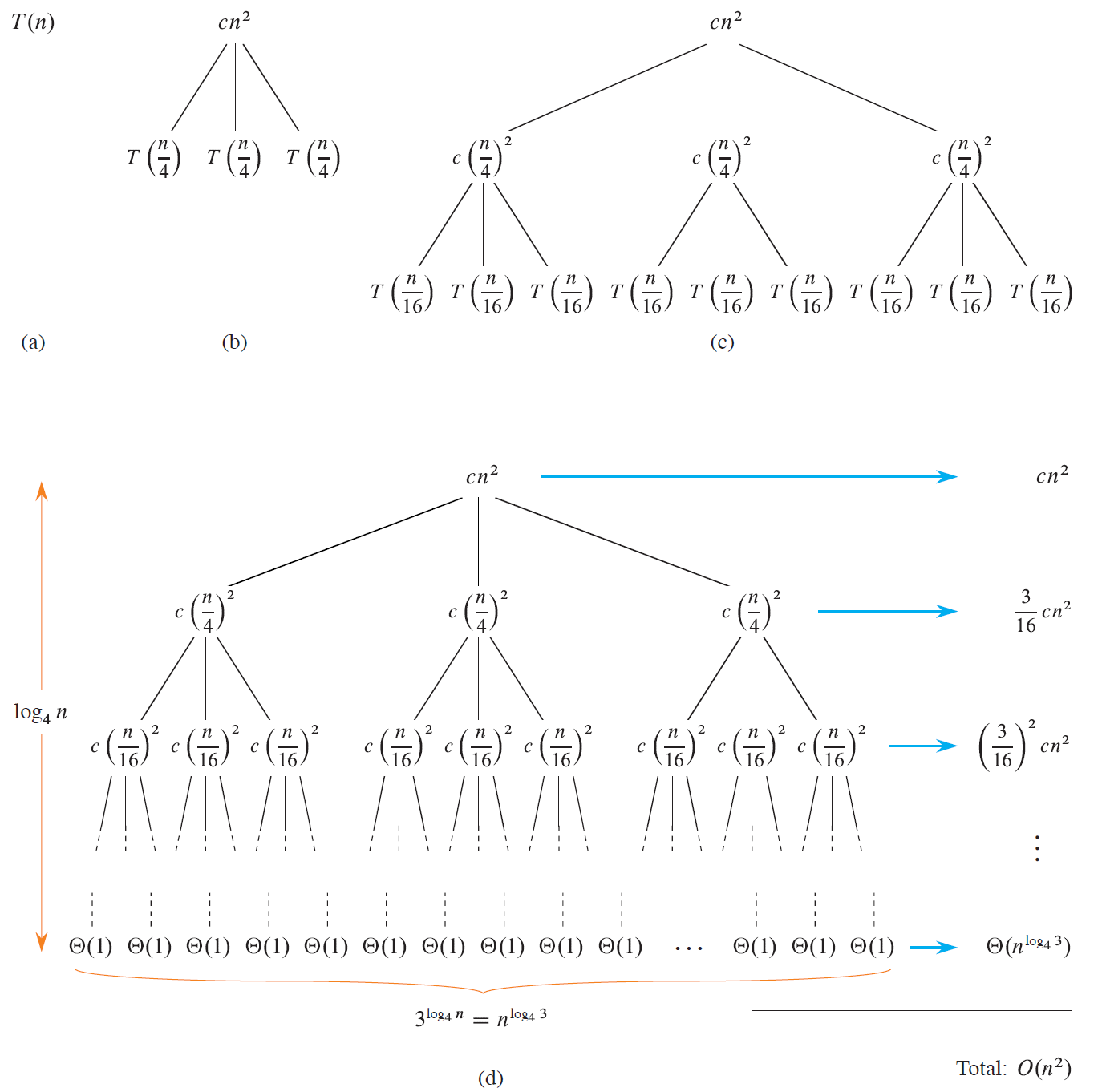
同样使用以下这个递归来演示递归树法是如何计算时间复杂度的

$$T(n)=3T(n/4)+\Theta(n^2)$$

主方法

提示

对于递归等式 T(n) = aT(n/b) + f(n), 其中 a > 0, b > 1 且对于任意大n满足f(n)非负，其时间复杂度计算可以根据以下情况分类

1. 如果存在ε>0使得

$$f(n)=\mathcal{O}(n^{log_b a-\epsilon})$$

则

$$T(n) = \Theta(n^{log_ba})$$

2. 如果存在k >= 0 使得

$$f(n)=\Theta(n^{log_ba}lg^kn)$$

则

$$T(n)=\Theta(n^{log_ba}lg^{k+1}n)$$

3. 如果存在ε>0使得

$$f(n)=\Omega(n^{log_ba+\epsilon})$$

并且f(n)满足 af(n/b) <= cf(n)，其中 c < 1, 则

$$T(n) = \Theta(f(n))$$

Akra-Bazi法

提示

Akra-Bazi是主方法的一般化形式，用于解决如下的递归等式

$$T(n) = \sum_{i=1}^k a_iT(n/b_i) + f(n)$$

当f(n)满足多项式成长的条件，则

$$T(n)=\Theta\left(n^p\left(1 + \int_1^n\frac{f(x)}{x^{p+1}}dx\right)\right)$$

其中 p 满足

$$\sum_{i=1}^k \frac{a_i}{b_i^p} = 1$$