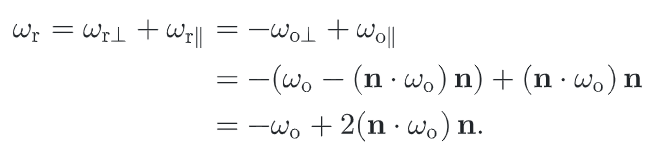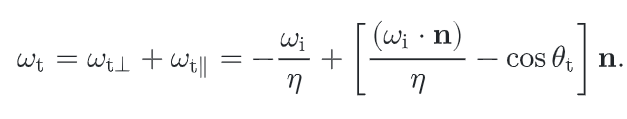Lambertian 漫反射模型
这是最简单的 BRDF 模型之一,描述了一个完美的漫反射表面,入射光经过该表面向各个方向反射的辐射度都相同。反射率 albedo 定义如下
ρalbedo=∫H2(n)fr(p,ωo,ωi)cosθidωi
其表示半球上的常量入射光经过物体表面反射到某一给定方向 ωo 上的比例,又根据 BRDF 的可逆性,也等价于表示某一给定方向的入射光经过物体表面反射到整个半球面上的比例
又因为 fr(p,ωo,ωi) 是常量,可得
fr(p,ωo,ωi)=πρalbedo
单位圆的面积等于 π,因此根据面积均匀采样的 PDF p(x,y)=1/π,变换到极坐标后可得 p(r,θ)=r/π,我们可以计算边际和条件概率密度:
p(r)p(θ∣r)=∫02πp(r,θ)dθ=2r=p(r)p(r,θ)=2π1
CDF 等于
P(r)P(θ∣r)=∫0r2r′dr′=r2=∫0θ2π1dθ′=2πθ
根据反转方法采样,可得
提示
rθ=ξ1=2πξ2
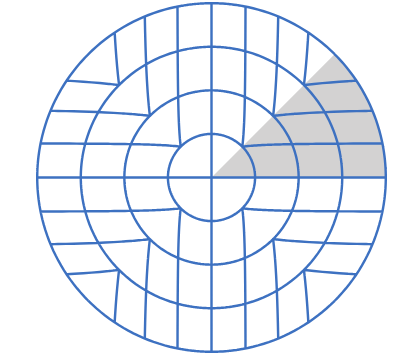
虽然该映射方法可以解决问题,但是如下图所示会扭曲在圆上的面积
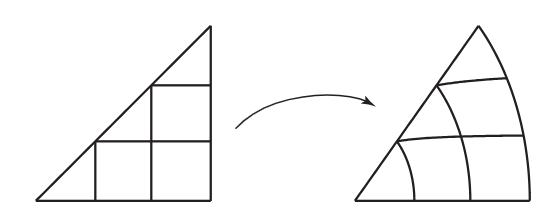
同心映射可以解决扭曲的问题
例如上图中阴影区域通过以下公式映射到 (r,θ)
rθ=x=xy4π
Point2f SampleUniformDiskConcentric(Point2f u) {
// 将 u 映射到 [-1, 1]x[-1, 1] 并且处理原点处的退化
Point2f uOffset = 2 * u - Vector2f(1, 1);
if (uOffset.x == 0 && uOffset.y == 0)
return {0, 0};
// 应用同心映射
Float theta, r;
if (std::abs(uOffset.x) > std::abs(uOffset.y)) {
r = uOffset.x;
theta = PiOver4 * (uOffset.y / uOffset.x);
} else {
r = uOffset.y;
theta = PiOver2 - PiOver4 * (uOffset.x / uOffset.y);
}
return r * Point2f(std::cos(theta), std::sin(theta));
}
单位半球面的面积是 2π,因此均匀采样半球面的 PDF p(ω)=1/(2π),下面使用球面坐标来推导采样算法:
由于
p(r,θ,ϕ)=r2sinθp(x,y,z)
则
p(θ,ϕ)=sinθ/(2π)
该密度函数是可分离的,因为 ϕ 的范围是 0 - 2π 并且 p(ϕ)=1/(2π),因此 p(θ)=sinθ。这两个的 CDF 等于
P(θ)P(ϕ)=∫0θsinθ′dθ′=1−cosθ=∫0ϕ2π1dϕ′=2πϕ
根据反转方法采样,获取均匀分布的随机数 ξ1∈[0,1] (并取 ξ1=1−ξ1)和 ξ2∈[0,1],通过求逆可得采样的值等于
θϕ=cos−1ξ1=2πξ2
转换回笛卡尔坐标系,得到最终的采样公式:
提示
xyz=sinθcosϕ=cos(2πξ2)1−ξ12=sinθsinϕ=sin(2πξ2)1−ξ12=cosθ=ξ1
许多光传输积分公式包含一个余弦因子,根据重要性采样性质,有一种根据半球面的余弦加权分布生成方向的方法会很有用,该方法会更有可能采样得到接近球顶附近的方向。从数学上来讲,这意味着
p(ω)∝cosθ
进行归一化
∫H2p(ω)dω∫02π∫02πccosθsinθdθdϕc2π∫0π/2cosθsinθdθc=1=1=1=π1
因此
p(ω)=π1cosθ
我们可以是使用 Malley 方法来采样该分布
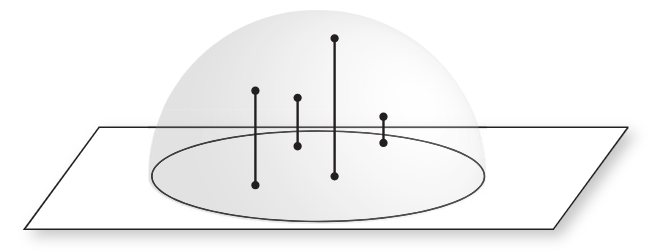
Malley 方法
从单位圆中均匀采样点,然后将该点向上投影到半球面上,如此获得的采样点即满足余弦加权分布
定义
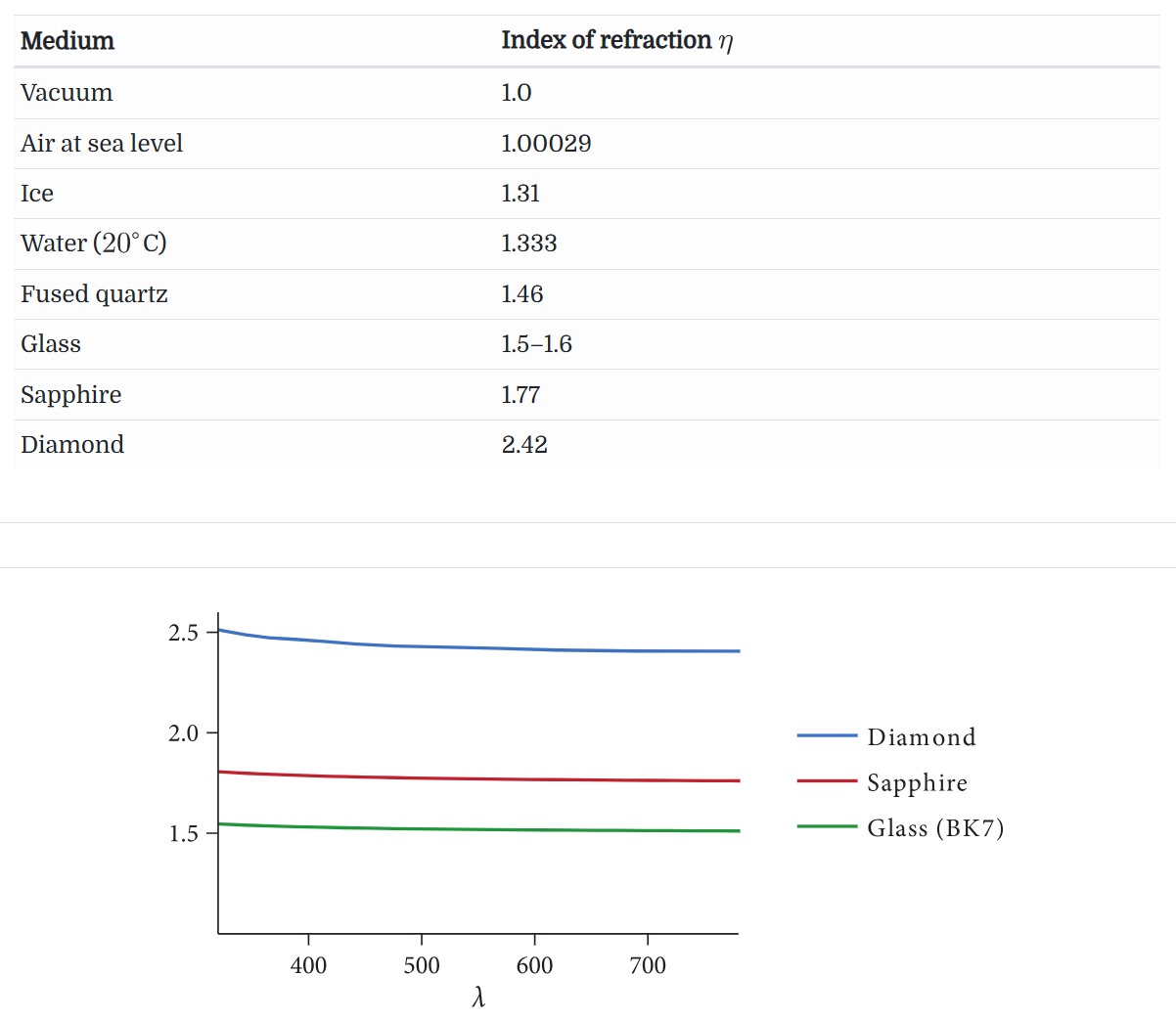
通常用折射率 IOR 来概括光的速度降低,例如,光遇到折射率等于 2 的材质表面后速度会降为原来的一半。折射率的范围通常在 1.0 - 2.5 之间且随光的波长而变化,用希腊字母 η 表示。
当光遇到 IOR 值突然变化的边界时会发生明显的反射,折射率 η 控制了表面的外观表现,因此对于该值的良好估计对于基于物理的渲染非常重要。
给定入射光的方向 (θi,ϕi),完美镜面的反射方向 (θr,ϕr) 满足以下性质:
θrϕr=θi=ϕi+π
也可以使用向量来计算
定义
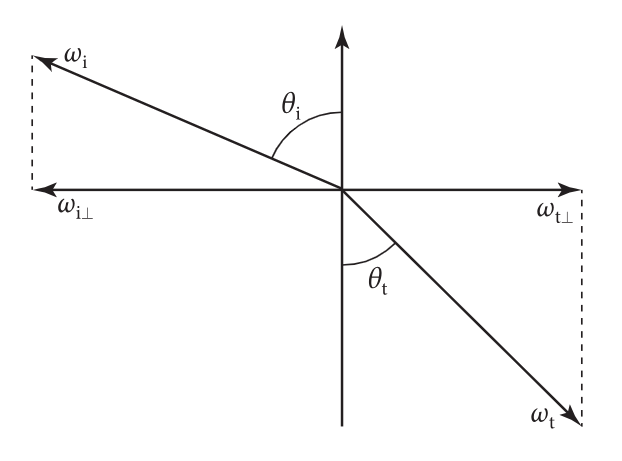
斯涅尔定律描述了光的入射方向 (θi,ϕi) 和透射方向 (θt,ϕt) 之间的关系,依赖于边界两边介质的折射率 ηi 和 ηt,满足如下性质:
ηisinθiϕt=ηtsinθt=ϕi+π
一个有用的观察:斯涅尔定律不依赖于具体的 ηi 和 ηt 的值,而是他们的比值,因此该定律也可以写成
sinθi=ηsinθt
其中 η=ηiηt 表示相对折射率
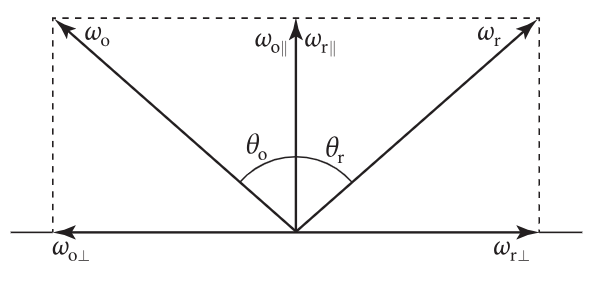
同样也可以使用向量来计算
r∥=ηtcosθi+ηicosθtηtcosθi−ηicosθtr⊥=ηicosθi+ηtcosθtηicosθi−ηtcosθt
同样也可以用相对折射率来表示
r∥=ηcosθi+cosθtηcosθi−cosθt,r⊥=cosθi+ηcosθtcosθi−ηcosθt
菲涅尔反射
Fr=21(r∥2+r⊥2)
提示
导体的折射率 IOR 是一个复数,其中实数部分和之前一样描述光的速度降低,而虚数部分描述光在导体内部传播过程中的衰减。这个衰减非常快,对反射的多少也有显著影响,因此我们也必须考虑这个因素。
导体的折射率可以表示为 η−ik,其中 k 表示吸收系数,入射和出射光都可以用平面波来建模描述随时间和距离 z 而变化的震荡,例如
E(z)=e−iα(η−ik)z=e−iαηze−αkz
其实数部分等于
e−αkzcos(αηz)
下图是黄金的折射率和吸收系数(都依赖于光的波长)
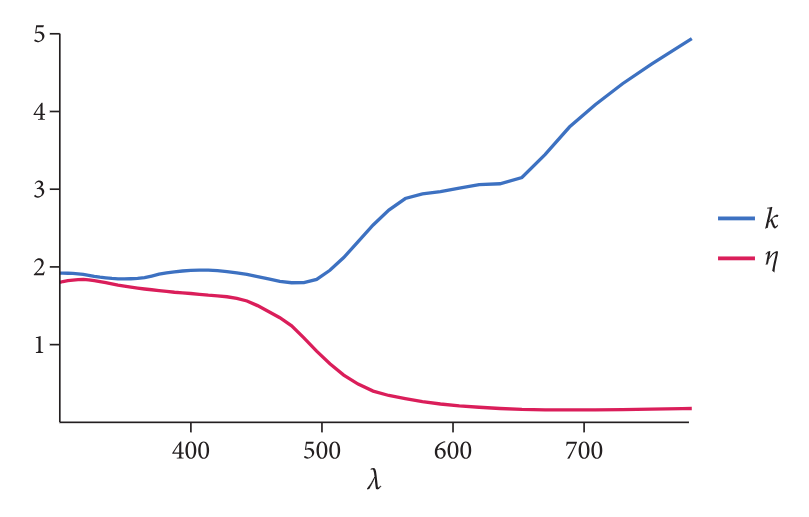
相关信息
导体 BRDF 基于两个物理概念:镜面反射定律决定每条光线的反射方向,以及菲涅尔等式决定反射光的比例。剩余的光会折射到导体中,被快速吸收并转化为热量。
令 Fr(ω) 表示来自 ω 方向光的菲涅尔反射比例,我们需要求解 BRDF fr 使得满足以下等式:
Lo(ωo)=∫H2(n)fr(ωo,ωi)Li(ωi)∣cosθi∣dωi=Fr(ωr)Li(ωr)
根据 Dirac delta 分布性质
∫f(x)δ(x−x0)dx=f(x0)
可以猜测导体 BRDF 等于
fr(ωo,ωi)=δ(ωi−ωr)Fr(ωi)
代入可得
Lo(ωo)=∫H2(n)δ(ωi−ωr)Fr(ωi)Li(ωi)∣cosθi∣dωi=Fr(ωr)Li(ωr)∣cosθr∣
综上
导体 BRDF
fr(p,ωo,ωi)=Fr(ωr)∣cosθr∣δ(ωi−ωr)

相关信息
电介质的相对折射率是实数,因此除了反射之外还必须考虑折射的情况