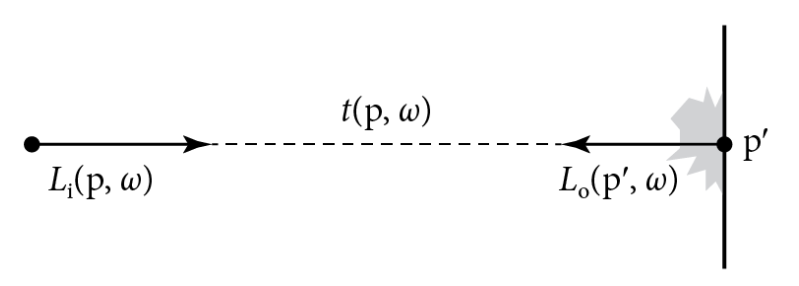光线传播 I：表面反射

光线传播公式 LTE

1. 基本推导

LTE 背后的关键原则是能量守恒，在宏观层面上有

$$\Phi_o - \Phi_i = \Phi_e - \Phi_a$$

为了在表面实现能量平衡，出射辐射度 $L_o$ 必须等于发射辐射度加上入射辐射度中被散射的部分

$$L_o(p,\omega_o) = L_e(p,\omega_o) + \int_{S^2} f(p,\omega_o,\omega_i) L_i(p,\omega_i) |cos\theta_i| d\omega_i$$

由于我们暂时假设不存在参与介质，所以光线在场景中沿直线传播的过程中辐射度是恒定不变的。因此，我们可以将点 p 处的入射辐射度与另一点 p' 处的出射辐射度关联起来。我们将光线投射函数 $t(p,\omega)$ 定义为从点 p 处沿着 $\omega$ 方向发出的光线与第一个表面相交的点 p'，则有

$$L_i(p,\omega) = L_o(t(p,\omega),-\omega)$$

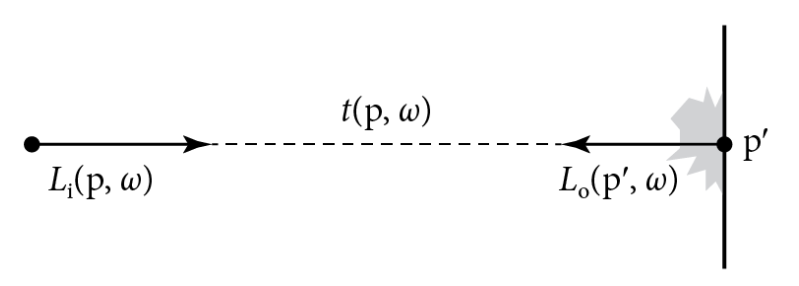
由上，LTE 可以写成

$$L(p,\omega_o) = L_e(p,\omega_o) + \int_{S^2} f(p,\omega_o,\omega_i) L(t(p,\omega_i),-\omega_i)|cos\theta_i| d\omega_i$$

2. LTE 的面积积分形式

首先，我们将从点 p' 到点 p 的出射辐射度定义为

$$L(p' \rightarrow p) = L(p',\omega)$$

如果 p' 和 p 互相可见并且定义 $\omega = \widehat{p - p'}$，我们也可以将点 $p'$ 处的 BSDF 写成

$$f(p^{\prime \prime} \rightarrow p^{\prime} \rightarrow p)=f(p^{\prime}, \omega_{o}, \omega_{i})$$

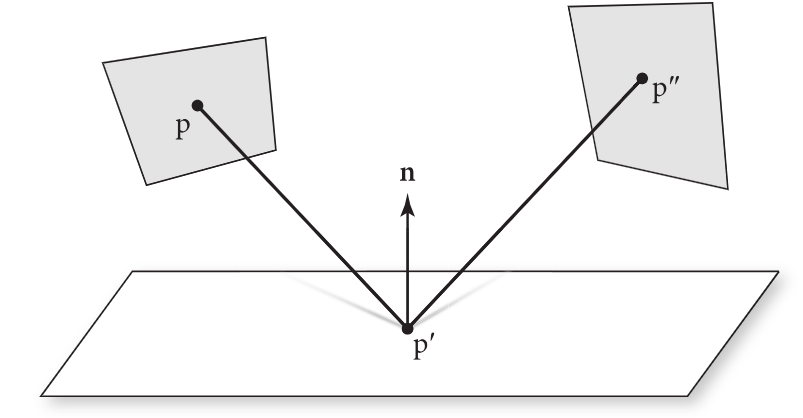
为了将 LTE 从方向上的积分转换为表面面积上的积分，我们还需要乘上将立体角与面积联系起来的雅可比项 $|cos\theta'|/r^2$

我们将这个变量变化项，LTE 中原始的 $|cos\theta|$ 和二元可见性函数 $V$ 组合成一个几何项 $G(p \leftrightarrow p')$

$$G(p \leftrightarrow p') = V(p \leftrightarrow p') \frac{|cos\theta| |cos\theta'|}{\|p - p'\|^2}$$

代入 LTE 将其转换成表面面积上的积分

$$L(p' \rightarrow p) = L_e(p' \rightarrow p) + \int_A f(p^{\prime \prime} \rightarrow p' \rightarrow p) L(p^{\prime \prime} \rightarrow p') G(p^{\prime \prime} \leftrightarrow p') dA(p^{\prime \prime})$$

其中 $A$ 表示场景中的所有表面

3. 路径积分

利用上述公式的面积积分形式，我们可以推导出更灵活的 LTE 形式，即光线传播的路径积分公式，它将辐射度表示为路径上的积分，而路径本身就是高维路径空间中的点。使用路径空间的主要动机之一是，它为测量值提供了一个显式路径积分表达式，而不是能量平衡方程推导出的笨拙的递归定义。

为了从面积积分转化为路径积分之和，我们可以展开上述 LTE，反复将方程的右边替换为积分中 $L(p^{\prime \prime} \rightarrow p')$ 项中

$$\begin{aligned} L(p_1 \rightarrow p_0) = &L_e(p_1 \rightarrow p_0) \\ &+ \int_A L_e(p_2 \rightarrow p_1) f(p_2 \rightarrow p_1 \rightarrow p_0) G(p_2 \leftrightarrow p_1) dA(p_2) \\ &+ \int_A\int_A L_e(p_3 \rightarrow p_2) f(p_3 \rightarrow p_2 \rightarrow p_1) G(p_3 \leftrightarrow p_2)\\[10px] &\quad\quad \times f(p_2 \rightarrow p_1 \rightarrow p_0) G(p_2 \leftrightarrow p_11) dA(p_3)dA(p_2) + \cdots \end{aligned}$$

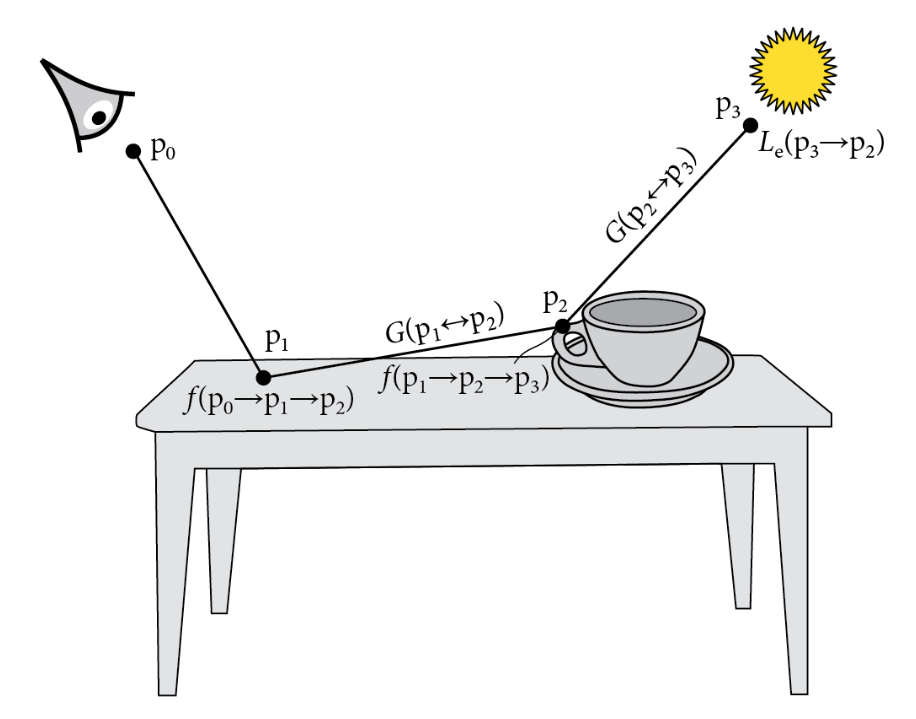
该无穷和可以简写为

$$L(p_1 \rightarrow p_0) = \sum_{n=1}^\infty P(\bar{p}_n) , \quad \bar{p}_n = p_0,p_1,...,p_n$$

其中 $P(\bar{p}_n)$ 表示沿着路径 $\bar{p}_n$ 散射的辐射度

$$\begin{aligned} P(\bar{p}_n) &= \underbrace{\int_A\int_A\cdots\int_A}_{n-1} L_e(p_n \rightarrow p_{n-1}) \\ &\quad\quad \times \left(\prod_{i=1}^{n-1}f(p_{i+1} \rightarrow p_i \rightarrow p_{i-1})G(p_{i+1} \leftrightarrow p_i)\right) dA(p_2)\cdots dA(p_n) \end{aligned}$$

令

$$T(\bar{p}_n) = \prod_{i=1}^{n-1} f(p_{i+1} \rightarrow p_i \rightarrow p_{i-1}) G(p_{i+1} \leftrightarrow p_i)$$

表示从光源发出的辐射经过所有这些路径散射之后到达相机的比例，则有

$$P(\bar{p}_n) = \underbrace{\int_A\int_A\cdots\int_A}_{n-1} L_e(p_n \rightarrow p_{n-1}) T(\bar{p}_n) \; dA(p_2)\cdots dA(p_n)$$

路径追踪

1. 概述

给定 LTE 的路径积分形式，我们想要估算出从点 $p_1$ 发出到相机 $p_0$ 的辐射度，

$$L(p_1 \rightarrow p_0) = \sum_{i=1}^\infty P(\bar{p}_i)$$

对于路径追踪，我们可以利用这样一个事实：对于物理上有效的场景，路径的顶点越多，最终散射的光越少。因此，我们始终估计前几项 $P(\bar{p}_i)$，然后应用俄罗斯轮盘，在有限数量的项之后停止采用，而不会引入偏差。例如，如果我们始终计算 $P(\bar{p}_1)$，$P(\bar{p}_2)$，$P(\bar{p}_3)$，但是以概率 q 停止计算后面的项，那么整个路径的无偏估计值等于

$$P(\bar{p}_1) + P(\bar{p}_2) + P(\bar{p}_3) + \frac{1}{1-q} \sum_{i=4}^\infty P(\bar{p}_i)$$

如果我们更进一步，随机考虑对于每一项以概率 $q_i$ 停止计算，那么整个路径的无偏估计值等于

$$\frac{1}{1-q_1} \left( P(\bar{p}_1) + \frac{1}{1 - q_2} \left( P(\bar{p}_2) + \frac{1}{1-q_3}(P(\bar{p}_3) + \cdots, \right. \right.$$

2. 路径采样

提示

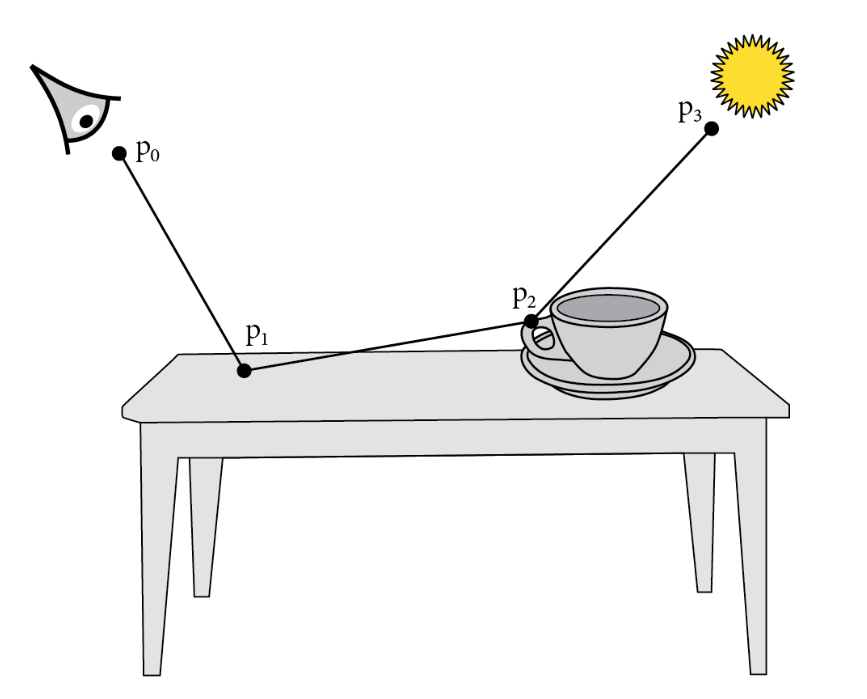
我们需要一种方法来估计路径 $P(\bar{p}_i)$ 的贡献，其中最后一个点 $p_i$ 在一个光源上，第一个点 $p_0$ 在相机或镜头上。最自然的做法是根据场景中物体的表面积对顶点进行采样，以便场景中所有表面上的点都以相同的概率进行采样。

假设每个表面的面积等于 $A_i$，则采样的顶点在第 i 个对象表面的概率等于

$$p_i = \frac{A_i}{\sum_j A_j}$$

然后，以均匀概率对第 i 个对象上的点进行采样，概率密度函数 PDF 等于 $1/A_i$，则采样场景中任意一点的概率密度函数等于

$$p_A(p_i) = \frac{A_i}{\sum_j A_j} \frac{1}{A_i} = \frac{1}{\sum_j A_j}$$

注意

然而，使用这种方式采样路径存在两个相互关联的问题：

1. 使用该方式采样得到的路径中存在大量对结果没有贡献的路径（当存在相邻两个顶点互相不可见时），例如在一个复杂的建筑模型场景中时，任意两个顶点之间几乎都存在墙，因此导致估计的方差很大。

2. 第二个问题是如果被积函数中有 delta 函数时（例如一个点光源或者完美镜面 BSDF），使用该方式采样将永远不会选到令 delta 函数非零的路径。即使没有 delta 函数，随着 BSDF 变得越来越光滑，几乎所有路径的贡献都会很低，这是因为 $f(p_{i+1} \rightarrow p_i \rightarrow p_{i-1})$ 中的点会导致 BSDF 具有很小的值或者为零，从而又会导致估计的方差很大。

3. 增量路径构建

提示

解决这两个问题的一种解决方案是从相机的顶点 $p_0$ 开始逐步构建路径，在每个顶点 $p_i$ 处，对 BSDF 进行采样以生成一个新的方向，然后在该方向上进行光线追踪找到最近的交点作为下一个顶点 $p_{i+1}$

由于此方法是根据立体角采样 BSDF 来构建路径，而路径积分 LTE 是对场景中表面面积的积分，因此我们需要应用校正将根据立体角的概率密度转换为根据面积的概率密度。如果 $\omega_{i-1}$ 是在顶点 $p_{i-1}$ 处采样的归一化方向，则

$$p_A(p_i) = p_\omega(\omega_{i-1})\frac{|cos\theta_i|}{\|p_{i-1} - p_i\|^2}$$

使用路径追踪时，路径的最后一个顶点（位于光源表面）会得到特殊处理，它不是以增量方式采样，而是从光源表面的分布中进行采样。现在我们假设发射器存在一种采样分布 $p_e$，后面我们将看到一个更有效的使用多重重要性采样的估计。

使用这种方法，路径的蒙特卡洛估计值等于

$$\begin{aligned} P(\bar{p}_i) &\approx \frac{L_e(p_i \rightarrow p_{i-1}) f(p_i \rightarrow p_{i-1} \rightarrow p_{i-2}) G(p_i \leftrightarrow p_{i-1})}{p_e(p_i)} \\ & \quad\quad \times \left(\prod_{j=1}^{i-2}\frac{f(p_{j+1} \rightarrow p_j \rightarrow p_{j-1})G(p_{j+1} \leftrightarrow p_j)}{p_A(p_{j+1})}\right) \end{aligned}$$

而

$$G(p_{j+1} \leftrightarrow p_j) = V(p_{j+1} \leftrightarrow p_j) \frac{|cos\theta_j||cos\theta_{j+1}|}{\|p_{j+1} - p_j\|^2} = \frac{|cos\theta_j||cos\theta_{j+1}|}{\|p_{j+1} - p_j\|^2}$$

$$p_A(p_{j+1}) = p_\omega(\omega_{j})\frac{|cos\theta_{j+1}|}{\|p_{j+1} - p_j\|^2}$$

综上

$$\begin{aligned} P(\bar{p}_i) &\approx \frac{L_e(p_i \rightarrow p_{i-1}) f(p_i \rightarrow p_{i-1} \rightarrow p_{i-2}) G(p_i \leftrightarrow p_{i-1})}{p_e(p_i)} \\ & \quad\quad \times \left(\prod_{j=1}^{i-2}\frac{f(p_{j+1} \rightarrow p_j \rightarrow p_{j-1})|cos\theta_j|}{p_\omega(\omega_j)}\right) \end{aligned}$$

由于此采样方案在构建长度路径时重复使用了长度路径的顶点（发射器上的顶点除外），因此它确实在项之间引入了相关性，但这不会影响蒙特卡洛估计的无偏性。