相关信息
微平面理论将粗糙的平面建模成为一组微平面的集合,每一个单独的微平面都非常小,无法被相机分辨,然而这些微平面的集合对于散射光的角度分布却有着巨大的影响。
微平面模型主要由两部分组成:
- 微平面的法线统计分布
- 微平面的 BSDF
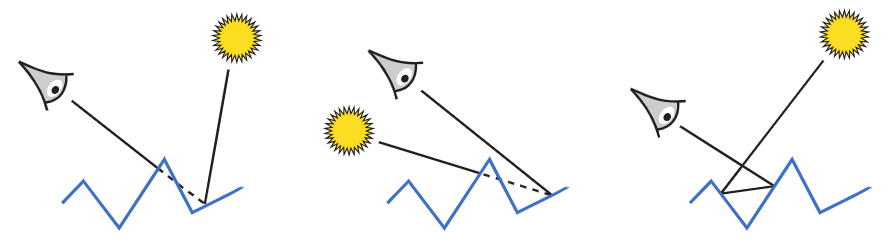
除此之外,以下三个因素也会对光的散射产生影响:遮挡、阴影和微平面间的反射
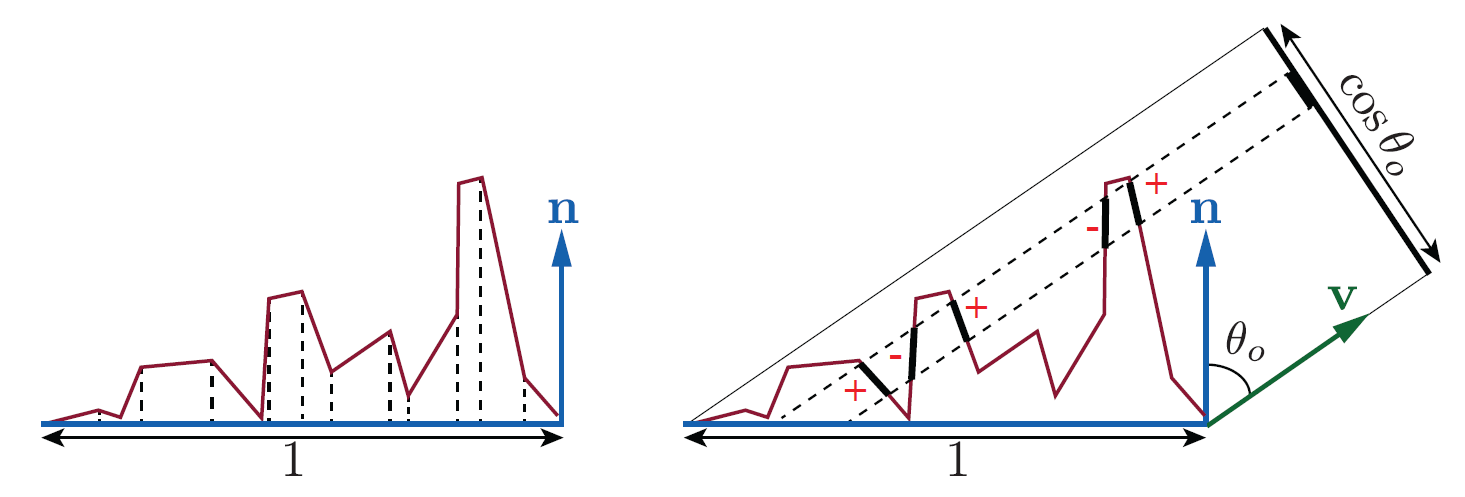
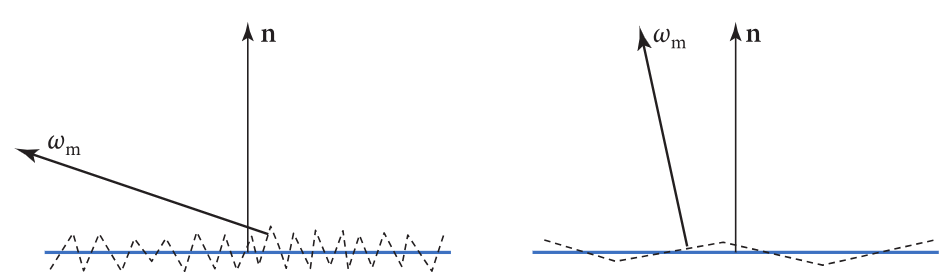
微平面的法线统计分布 NDF D(m) 表示在 1 个单位宏观面积下,方向角等于 ωm 的所有微平面的总面积,对方向角取微分可得:
dAm=D(m)dωmA
将 A 移到等式左边,两边同时积分可得:
A1∫(n⋅m)dAm=∫ΩD(m)(n⋅m)dωm
当上述等式为 1 时, 即 ∫(n⋅m)dAm=A,表示所有微平面的投影面积之和等于宏观平面面积,则得出 NDF 需要满足的一个性质:
NDF 性质 1
∫m∈ΘD(m)(n⋅m)dm=1
更一般地,投影到任意方向 v 满足如下性质
NDF 性质 2
∫m∈ΘD(m)(v⋅m)dm=v⋅n
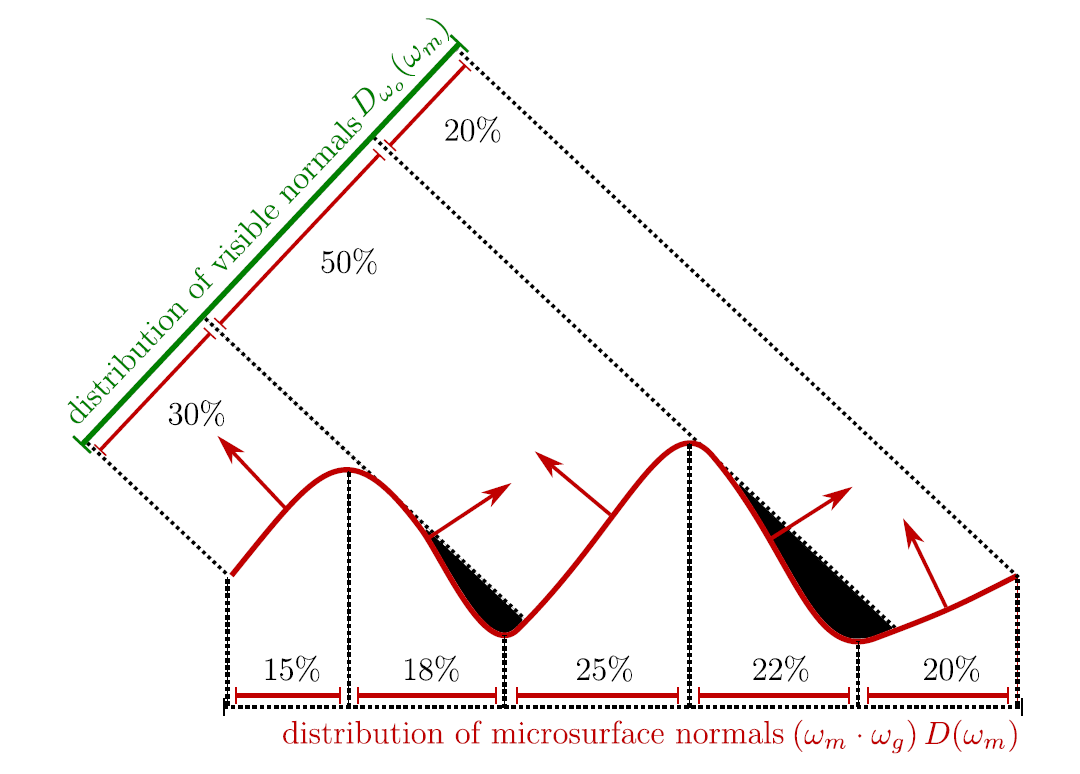
另外我们可以看到,存在许多重叠的微平面会投影到同一个区域,正负相互抵消之后我们只关心可见的那一个微平面(即最接近投影平面的那一个)。我们定义遮挡函数 G₁(m,v) 表示在所有法线等于 m 的微平面中,在 v 方向上可见的微平面所占的比例,则有
NDF 性质 3
∫m∈ΘG1(m,v)D(m)(v⋅m)+dm=v⋅n
Heitz 证明了只有 Smith 遮挡函数和 Torrance-Sparrow "V-cavity" 函数满足以上性质且在数学上是有效的;进一步的,Heitz 还证明了只有 Smith 遮挡函数同时满足 normal-masking 独立性,即 G₁(m,v) 不依赖于法线方向 m 只要 m·v ≥ 0
Smith G₁ 函数
G1(m,v)=1+Λ(v)χ+(m⋅v)
其中
χ+(x)={1,0,where x>0where x≤0
Λ 函数对于每一个 NDF 都不同
注意
Smith 遮挡函数适用于随机表面,对于法线和遮挡有强依赖的表面(尤其是具有重复结构的表面,例如大多数织物),其准确性则会降低。
类似地,我们可以定义联合遮挡-阴影函数 G₂(l,v,m) 表示在所有法线等于 m 的微平面中,在 l 和 v 方向上都可见的微平面所占的比例
G₂ 函数有多种形式
- 分离式
提示
G2(l,v,m)=G1(v,m)G1(l,m)
该形式表示遮挡和阴影是不相关的事件,这是不符合现实的,因此会导致表面显示过暗
- 方向相关
当 v 和 l 之间的水平夹角等于 0 时,G₂(l,v,m) 应该等于 min(G₁(m,v),G₁(m,l)),则
提示
G2(l,v,m)=λ(ϕ)G1(v,m)G1(l,m)+(1−λ(ϕ))min(G1(v,m),G1(l,m))
该等式表示了在分离式和高度相关之间的线性插值
- 高度相关
高度越低的点被遮挡和阴影的概率越大,如果使用 Smith 遮挡函数,则可以用 Smith 高度相关遮挡-阴影函数来表示该关联
提示
G2(l,v,m)=1+Λ(v)+Λ(l)χ+(m⋅v)χ+(m⋅l)
- 方向和高度相关
提示
G2(l,v,m)=1+max(Λ(v),Λ(l))+λ(v,l)min(Λ(v),Λ(l))χ+(m⋅v)χ+(m⋅l)
- 根据 BRDF 定义
f(l,v)=Li∣n⋅l∣dωidL(M)
- 将宏观平面 L(M) 用微平面 L(m) 来表示 (每个微平面投影的 Irradiance 总和除以投影面积),其中 Do(m) 表示在投影方向上的可见法线分布
L(M)=∣n⋅v∣1∫ΩL(m)G1(l,v)∣m⋅v∣D(m)dm=∫ΩL(m)Do(m)dm
- 对上式进行微分
dL(M)=∫ΩdL(m)Do(m)dm
- 同样根据 BRDF 定义,微平面 L(m) 可以表示为
dL(m)=fμ(l,v,m)∣m⋅l∣Lidωi
- 结合 3,4 可得
dL(M)=∫Ωfμ(l,v,m)cosθiLidωiDo(m)dm=Lidωi∫Ωfμ(l,v,m)∣m⋅l∣Do(m)dm
- 结合 1,5 可得
f(l,v)=Li∣n⋅l∣dωiLidωi∫Ωfμ(l,v,m)∣m⋅l∣Do(m)dm=∣n⋅l∣1∫Ωfμ(l,v,m)∣m⋅l∣Do(m)dm=∣n⋅l∣1∣n⋅v∣1∫Ωfμ(l,v,m)∣m⋅l∣G1(l,v)∣m⋅v∣D(m)dm
我们使用 G2 代替 G1
提示
f(l,v)=∣n⋅l∣1∣n⋅v∣1∫Ωfμ(l,v,m)G2(l,v,m)D(m)∣m⋅l∣∣m⋅v∣dm
其中 n 是宏观平面的法线,m 是微平面的法线
specular BSDF 反射一部分入射光的能量到方向 s 上,反射比例 ρ (即菲涅尔反射 F) 和反射方向 s 是入射方向 i 和局部表面法线 m 的函数,可以写成
fs(i,o,m)=Lidωi∣i⋅m∣dL(m)δωo(s,o)=LidωidL(m)∣i⋅m∣δωo(s,o)=ρ∣o⋅m∣δωo(s,o)
其中
δωo(s,o)={∞,0,s=ootherwise
表示 Dirac delta 函数,且满足如下等式
∫Ωg(o)δωo(s,o)dωo={g(s)0s=ootherwise
又 fs(i,o,m) 是以出射方向 s 为积分变量, 为了代入上一节的方程,我们需要使用微平面的法线和其对应的立体角作为积分变量
fs(i,o,m)=ρ∣o⋅m∣δωm(h(i,o),m)∂ωo∂ωh=ρ∣o⋅m∣δωm(h(i,o),m)4∣o⋅h∣1=F(h,i)∣o⋅m∣δωm(h(i,o),m)4∣o⋅h∣1
相关信息
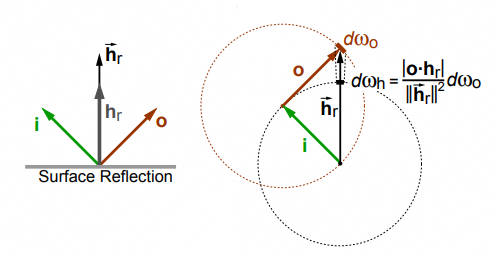
∂ωo∂ωh=∥hr2∥∣o⋅hr∣=(hr⋅hr)2∣o⋅hr∣=((i+o)⋅hr)2∣o⋅hr∣=(2o⋅hr)2∣o⋅hr∣=4∣o⋅h∣1
代入可得
提示
f(l,v)=∣n⋅l∣1∣n⋅v∣1∫ΩF(m,l)∣m⋅v∣δωm(h(l,v),m)4∣m⋅l∣1G2(l,v,m)D(m)∣m⋅l∣∣m⋅v∣dm=4∣n⋅l∣∣n⋅v∣F(h,l)G2(l,v,h)D(h)
fd(i,o,m)=π1
代入可得
提示
f(l,v)=π1∣n⋅l∣1∣n⋅v∣1∫ΩG2(l,v,m)D(m)∣m⋅l∣∣m⋅v∣dm
法线/遮挡独立性
Smith 假定微平面上不同点之间的法线或者高度是不相关的(即使是相邻点之间),是一组随机的不连续的微平面的集合。
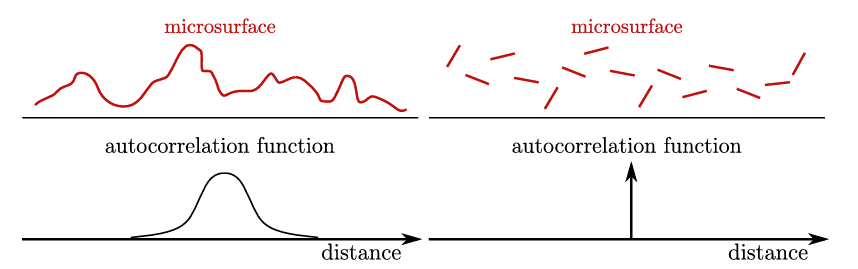
G1(ωo,ωm) 可以理解为被遮挡的概率,其独立于该点处的法线方向 ωm,因此可以表示为
G1(ωo,ωm)=G1local(ωo,ωm)G1dist(ωo)
其中
G1local=χ+(ωo⋅ωm)
遮挡函数公式推导
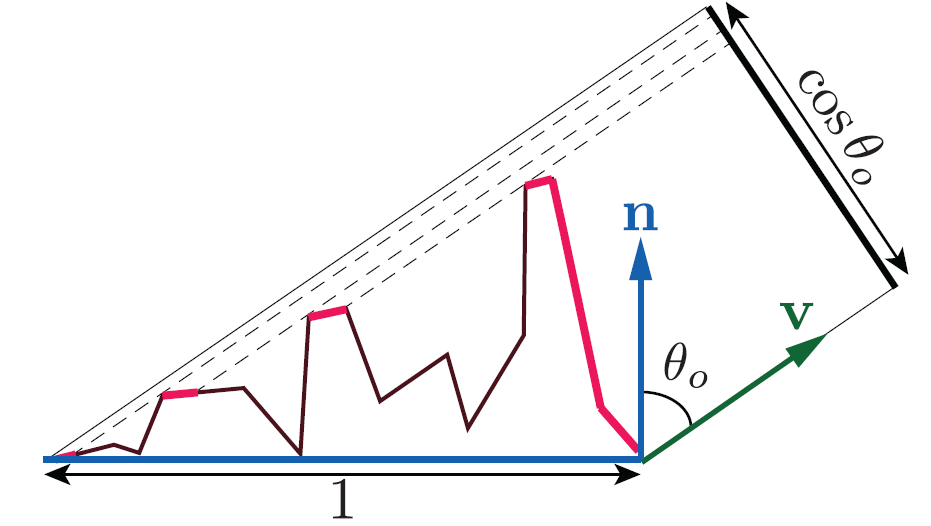
cosθo=∫ΩG1(ωo,ωm)(ωo,ωm)+D(ωm)dωm=∫ΩG1local(ωo,ωm)G1dist(ωo)(ωo,ωm)+D(ωm)dωm=∫Ωχ+(ωo⋅ωm)G1dist(ωo)(ωo,ωm)+D(ωm)dωm=G1dist(ωo)∫Ω(ωo,ωm)+D(ωm)dωm
可得
G1(ωo,ωm)=χ+(ωo⋅ωm)∫Ω(ωo,ωm)+D(ωm)dωmcosθo
通过将积分域从法线变换到斜率空间,可以证明 Smith 遮挡函数可以表示成
G1dist(ωo,ωm)=1+Λ(ωo)1
即
G1(ωo,ωm)=1+Λ(ωo)χ+(ωo⋅ωm)
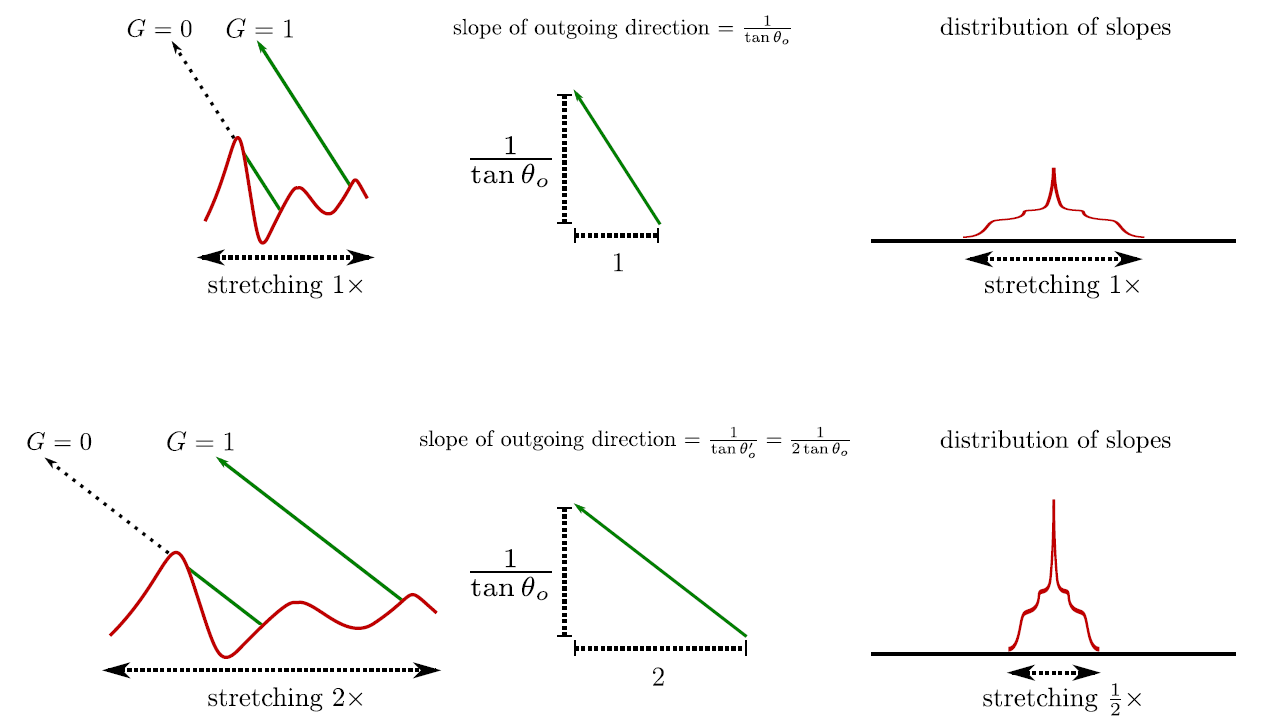
如果微平面是一个高度场,其高度分布表示为 P1(h),那么这个微平面的斜率就是高度的梯度,(xm~,ym~)=∇h, 斜率的分布可以表示为 P22(xm~,ym~)
m~=(xm~,ym~)=(−zmxm,−zmym)=−tanθm(cosϕm,sinϕm)
其中法线 ωm=(xm,ym,zm) 也可以用斜率表示为
ωm=xm~2+ym~2+1(−xm~,−ym~,1)
斜率分布必须满足归一化
∫−∞∞∫−∞∞P22(xm~,ym~)dxm~dym~=1
将积分域从斜率空间转换到法线空间后,法线分布可以表示为
D(ωm,α)=cos4θmP22(xm~,ym~,α)
其中 cos4θm1 表示 Jacobian 项,α 表示粗糙度参数
若干各向同性的斜率分布 P22 依赖于粗糙度参数 α, 且改变 α 等价于拉伸斜率的分布而不改变其形状。例如如下形式:
P22(xm~,ym~,α)=α21f((αxm~)2+(αym~)2)=α21f(αxm~2+ym~2)=α21f(αtanθm)
其中 f 是一维函数定义了分布的形状,α 是粗糙度参数,该形式满足如下性质:
P22(xm~,ym~,α)=λ21P22(λxm~,λym~,λα),∀λ>0
表示当 λα→α 变为原来的 λ 倍时,等价于斜率分布拉伸为原来的 λ 倍,即斜率 (λxm~,λym~) 拉伸到 (xm~,ym~) 且概率降低为 λ21。此时,遮挡函数只依赖于变量
a=αtanθo1
其中 tanθo1 表示出射方向的斜率
Beckmann 的斜率满足二维独立高斯分布和形状不变性,表示为
P22(xm~,ym~,σ)=2πσ21exp(−2σ2xm~2+ym~2)
则法线分布等于
D(ωm,σ)=2πσ2cos4θm1exp(−2σ2tan2θm)
令粗糙度参数 α=2σ,可得
提示
D(ωm,α)=πα2cos4θm1exp(−α2tan2θm)
GGX 的斜率满足二维独立 T 分布和形状不变性(T 分布是高斯分布的一般化形式并且具有更长的拖尾,当自由度 v→∞ 时,T 分布趋向于高斯分布),表示为
P22(xm~,ym~)=πα2(1+α2xm~2+ym~2)21
则法线分布等于
D(ωm,α)=πα2cos4θm(1+α2tan2θm)21=π(α2cos2θm+sin2θm)2α2
Λ 函数等于
Λ(ωo)=2−1+1+a21其中 a=αtanθo1
遮挡函数等于
G1(ωo,ωm)=1+Λ(ωo)1=1+1+a212=1+1+α2tan2θo2=cosθo+cos2θo+α2sin2θo2cosθo=cosθo+α2+(1−α2)cos2θo2cosθo
相关信息
在 Disney PBR 模型中,计算法线分布函数 D 时,使用粗糙度参数 α=r2;计算遮挡函数 G 时,使用粗糙度参数 α=(0.5+r/2)2,将 α 从 [0,1] 重新映射到 [0.5,1],避免过量的高光
根据高度相关的联合遮挡函数定义可得
G2(ωi,ωo,ωm)=1+Λ(ωi)+Λ(ωo)1=1+2−1+1+α2tan2θi+2−1+1+α2tan2θo1=1+α2tan2θi+1+α2tan2θo2
则
4cosθicosθoG2(ωi,ωo,ωm)=cosθicosθo(1+α2tan2θi+1+α2tan2θo)0.5=cosθoα2+(1−α2)cos2θi+cosθiα2+(1−α2)cos2θo0.5