线性时间排序

提示

基于比较的排序算法在最坏情况下至少需要比较 $\Omega(nlgn)$ 次

计数排序

counting_sort(A,n,k)
  let B[1:n] and C[0:k] be new arrays
  for i = 0 to k
    C[i] = 0
  for j = 1 to n
    C[A[j]] = C[A[j]] + 1
  // C[i] now contains the number of elements equal to i.
  for i = 1 to k
    C[i] = C[i] + C[i - 1]
  // C[i] now contains the number of elements less than or equal to i
  // Copy A to B, starting from the end of A
  for j = n downto 1
    B[C[A[j]]] = A[j]
    C[A[j]] = C[A[j]] - 1 // to handle duplicate values
  return B

提示

1. 计数排序假定输入是在小范围内的整数
2. 计数排序是稳定排序
3. 时间复杂度为 $\Theta(n+k)$

基数排序

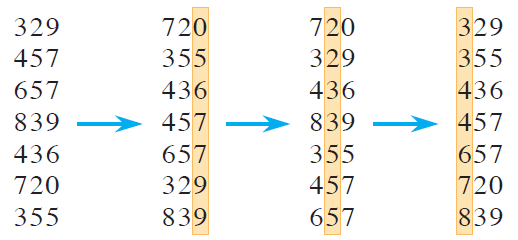
radix-sort(A,n,d)
  for i = 1 to d
    // commonly use counting sort
    use a stable sort to sort array A[1:n] on digit i

引理1

给定 n 个 d 位数字，每一位有 k 个取值范围，当使用时间复杂度为 $\Theta(n+k)$ 的稳定排序算法时，基数排序的时间复杂度为 $\Theta(d(n+k))$

引理2

给定 n 个 b 位二进制数字以及正整数 $r \le b$，当使用时间复杂度为 $\Theta(n+k)$ 的稳定排序算法时，基数排序的时间复杂度为 $\Theta((b/r)(n+2^r))$

当 $b < \lfloor lg n \rfloor$ 时，$r \le b$ 表示 $(n+2^r) = \Theta(n)$，则选择 $r = b$ 可得时间复杂度 $\Theta(n)$ 是渐进最优的

当 $b \ge \lfloor lgn \rfloor$ 时，选择 $r = \lfloor lgn \rfloor$，可得时间复杂度 $\Theta(bn/lgn)$ 是渐进最优的

桶排序

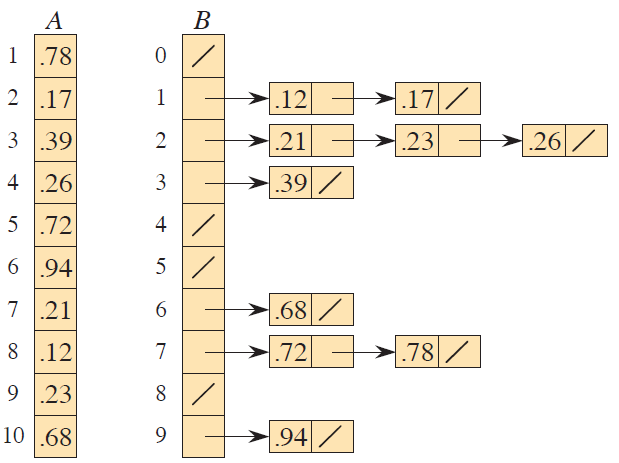
bucket_sort(A,n)    // 0 ≤ A[i] < 1
  let B[0:n-1] be a new array
  for i = 0 to n - 1
    make B[i] an empty list
  for i = 1 to n
    insert A[i] into list B[⌊n·A[i]⌋]
  for i = 0 to n - 1
    sort list B[i] with insertion sort
  concatenate the lists B[0],B[1],...,B[n-1] together in order
  return the concatenated listss

提示

1. 桶排序假定输入是 $[0,1)$ 内均匀独立分布的数字
2. 平均时间复杂度为 $\Theta(n)$

令随机变量 $n_i$ 表示落在桶 $B[i]$ 中的数量，则桶排序的运行时间为 $T(n) = \Theta(n) + \sum_{i=0}^{n-1}\mathcal{O}(n_i^2)$, 期望为

$$\begin{aligned} E[T(n)] &= E\left[\Theta(n) + \sum_{i=1}^{n-1} \mathcal{O}(n_i^2)\right] \\ &= \Theta(n) + \sum_{i=0}^{n-1} \mathcal{O}(E[n_i^2]) \\ &= \Theta(n) + n \cdot (2 - 1/n) \\ &= \Theta(n) \end{aligned}$$