中位数和顺序统计

选择问题

输入：n 个不同的数字和一个整数 i，1 ≤ i ≤ n
输出：第 i 大的元素 x

最小和最大

MINIMUM(A,n)
  min = A[1]
  for i = 2 to n
    if min > A[i]
        min = A[i]
  return min

提示

该算法是最优的，总共使用 n - 1 次比较操作

同时求出最小和最大

最多可以使用 $3\lfloor n/2 \rfloor$ 次比较操作，可以同时找到最小和最大值，主要思想为每次取 2 个元素并进行比较，将其中较小值和当前最小值进行比较，将其中较大值和当前最大值进行比较，总共使用 3 次比较。

期望线性时间选择算法

提示

使用类似于快速排序的分治算法，期望运行时间为 $\Theta(n)$，最坏运行时间为 $\Theta(n^2)$

RANDOMIZED-SELECT(A,p,r,i)
  if p == r
    return A[p]
  
  q = RANDOMIZED-PARTITION(A,p,r)
  k = q - p + 1
  if i == k
    return A[q]     // the pivot value is the answer
  else if i < k
    return RANDOMIZED-SELECT(A,p,q-1,i)
  else
    return RANDOMIZED-SELECT(A,q+1,r,i-k)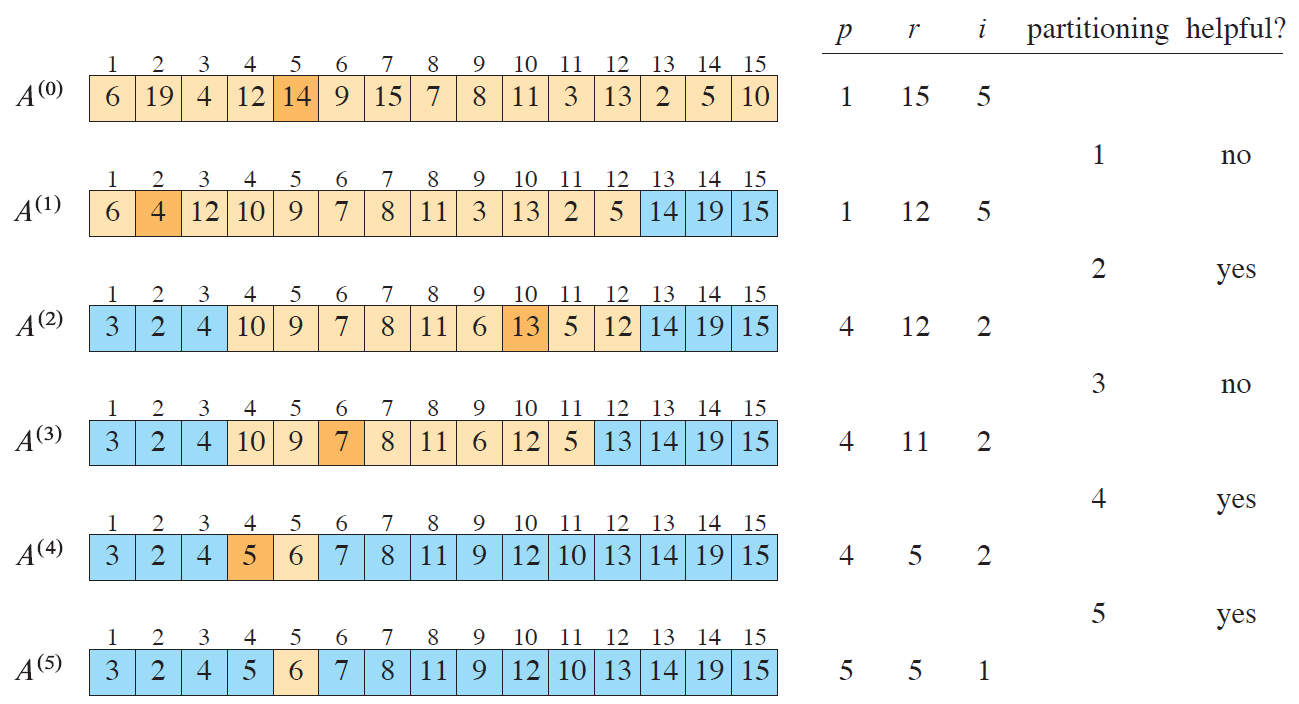

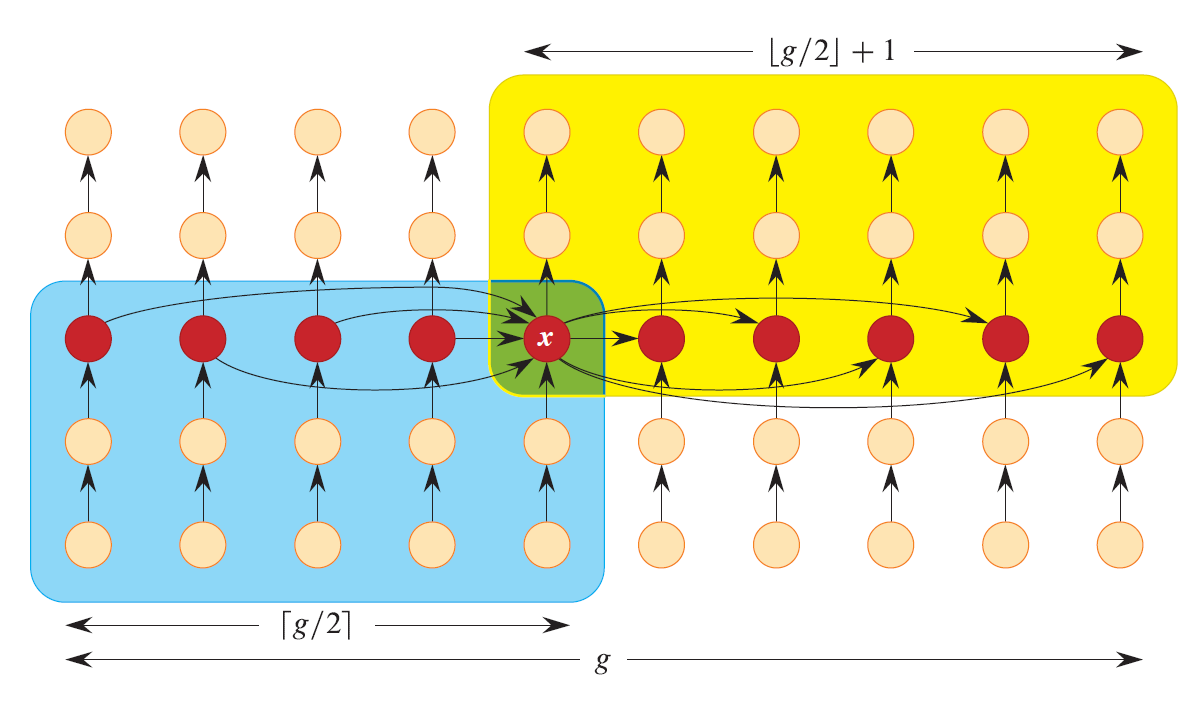
最坏情况线性时间选择算法

SELECT(A,p,r,i)
  while (r - p + 1) mod 5 ≠ 0
    for j = p + 1 to r          // put the minimum into A[p]
        if A[p] > A[j]
            exchange A[p] with A[j]
    // If we want the minimum of A[p:r], we're done.
    if i == 1
        return A[p]
    // Otherwise, we want the (i-1)st element of A[p+1:r].
    p = p + 1
    i = i - 1

  g = (r - p + 1) / 5           // number of 5-element groups
  for j = p to p + g - 1        // sort each group
    sort <A[j], A[j+g], A[j+2g], A[j+3g], A[j+4g]> in place

  // All group medians now lie in the middle fifth of A[p:r].
  x = SELECT(A,p+2g,p+3g-1,⌈g/2⌉)
  q = PARTITION-AROUND(A,p,r,x)

  // The rest is just like lines 3-9 of RANDOMIZED-SELECT.
  k = q - p + 1
  if i == k
    return A[q]
  else if i < k
    return SELECT(A,p,q-1,i)
  else
    return SELECT(A,q+1,r,i-k)