规则
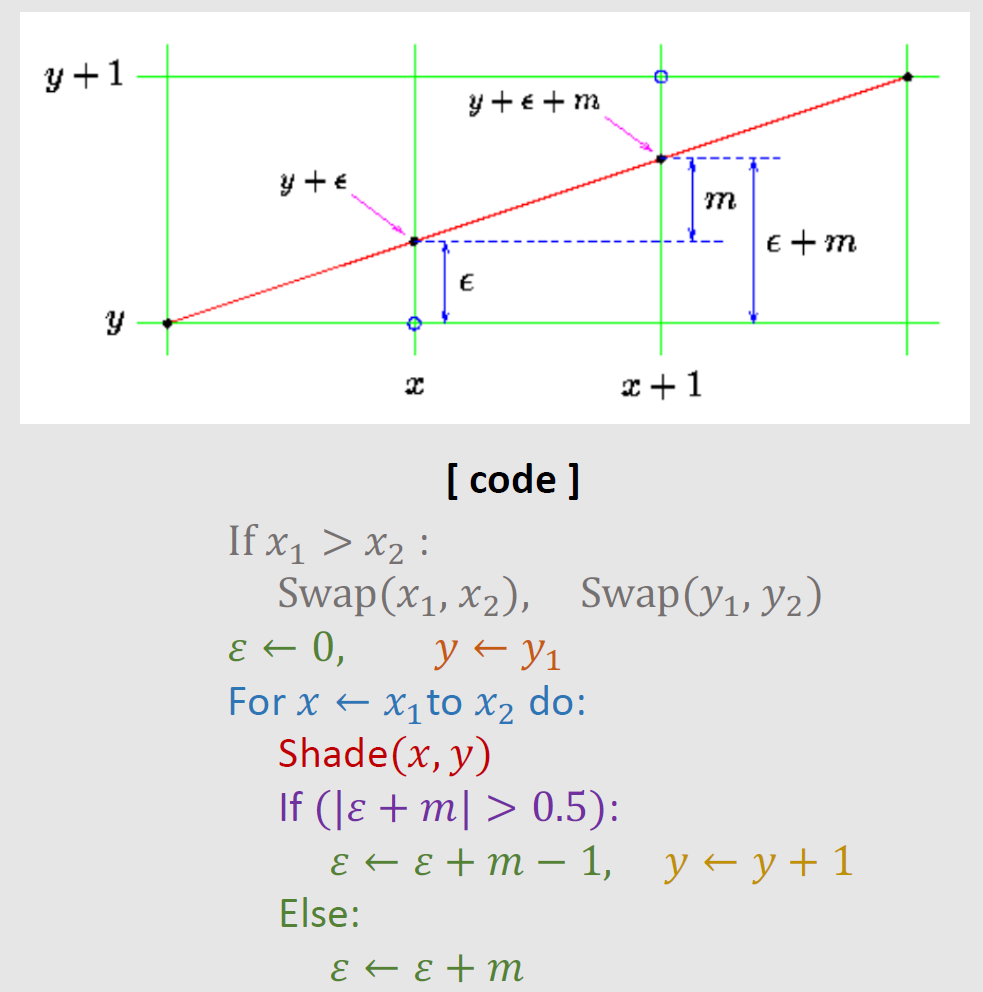
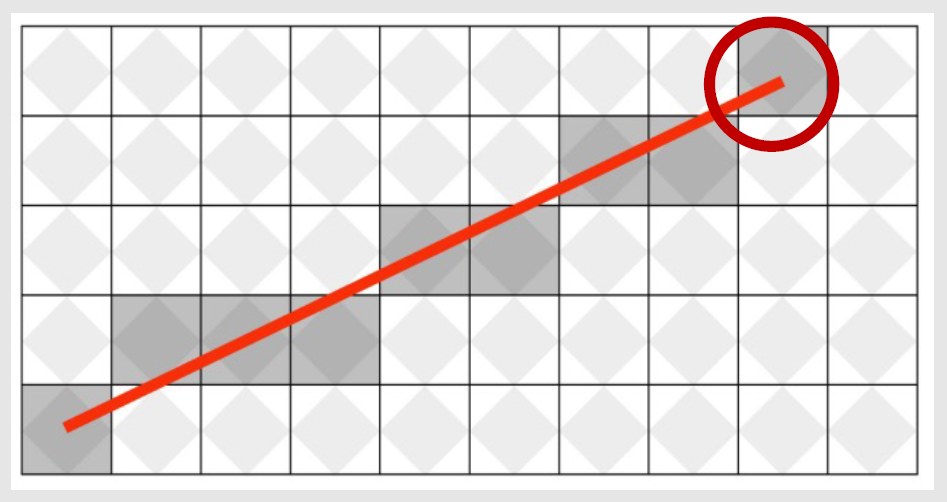
diamond-exit rule
对于每一个像素点,如果线段和该像素点内的钻石区域相交并且从该区域内穿出即(exit),则着色该像素点; 因此如果线段终点在像素钻石区域内,但没有穿出的话,那么也不着色该像素点,这样保证当有两段连续的线段连接在一起的时候,连接处的像素点只会绘制一次。
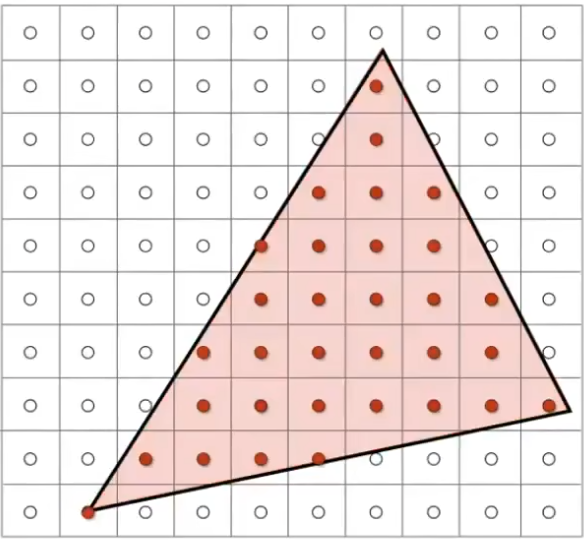
for (int x = xmin; x < xmax; ++x)
for (int y = ymin; y < ymax; ++y)
image[x][y] = inside(tri, x + 0.5, y + 0.5);
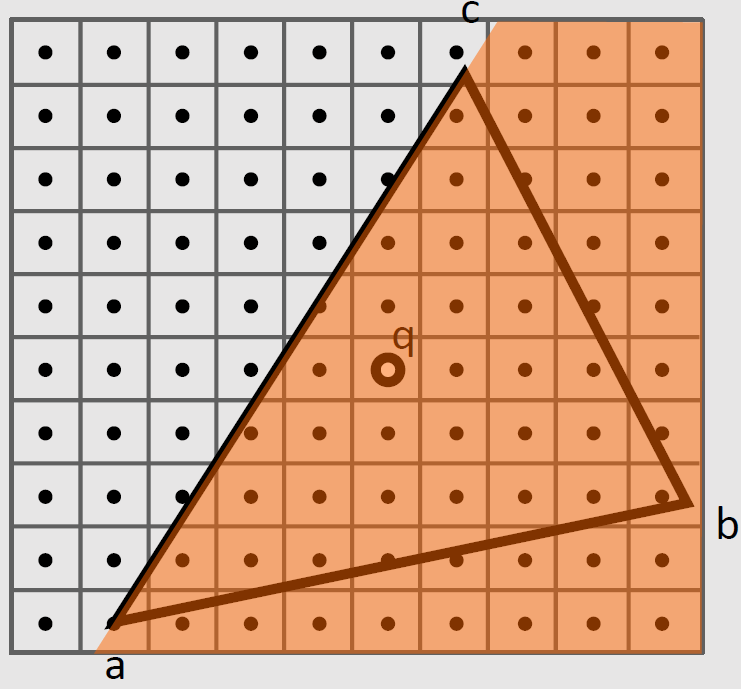
(ac×ab)⋅(ac×aq)>0
同理有
(cb×ca)⋅(cb×cq)>0(ba×bc)⋅(ba×bq)>0
警告
下面是一个种更简单的判断方法,不过三角形的顶点 A → B → C 必须是逆时针顺序(左右手坐标系都适用)!
[ab×aq]z>0[bc×bq]z>0[ca×cq]z>0
假设 P 是三角形 ABC 内一点,有
xpyp1=αxa+βxb+γxc=αya+βyb+γyc=α+β+γ
可得
αβγ=(xa−xc)(yb−yc)−(xb−xc)(ya−yc)(xp−xc)(yb−yc)−(xb−xc)(yp−yc)=(xb−xc)(ya−yc)−(xa−xc)(yb−yc)(xp−xc)(ya−yc)−(xa−xc)(yp−yc)=1−α−β
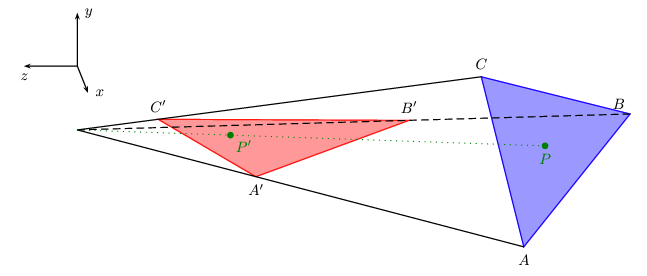
- 三角形 ABC 根据透视投影矩阵 M 变换到 A'B'C'
(A′wawa)(B′wbwb)(C′wcwc)(P′wpwp)=M(A1)=M(B1)=M(C1)=M(P1)
- P 和 P' 分别是三角形 ABC 和 A'B'C' 内的一点,有
PP′=αA+βB+γC=α′A′+β′B′+γ′C′
且
α+β+γα′+β′+γ′=1=1
- 结合 1 和 2 可得
(P1)M(P1)P′wpwp=α(A1)+β(B1)+γ(C1)=Mα(A1)+Mβ(B1)+Mγ(C1)=αA′wa+βB′wb+γC′wc=αwa+βwb+γwc
则
P′=αwa+βwb+γwcαA′wa+βB′wb+γC′wc=αwa+βwb+γwcαwaA′+αwa+βwb+γwcβwbB′+αwa+βwb+γwcγwcC′=α′A′+β′B′+γ′C′
从而有
α′β′γ′=αwa+βwb+γwcαwa=αwa+βwb+γwcβwb=αwa+βwb+γwcγwc
- 令
k=αwa+βwb+γwc1
可得
αβγ=wakα′=wbkβ′=wckγ′
又
1=α+β+γ=wakα′+wbkβ′+wckγ′
可得
kαβγ=waα′+wbβ′+wcγ′=waα′+wbβ′+wcγ′waα′=waα′+wbβ′+wcγ′wbβ′=waα′+wbβ′+wcγ′wcγ′