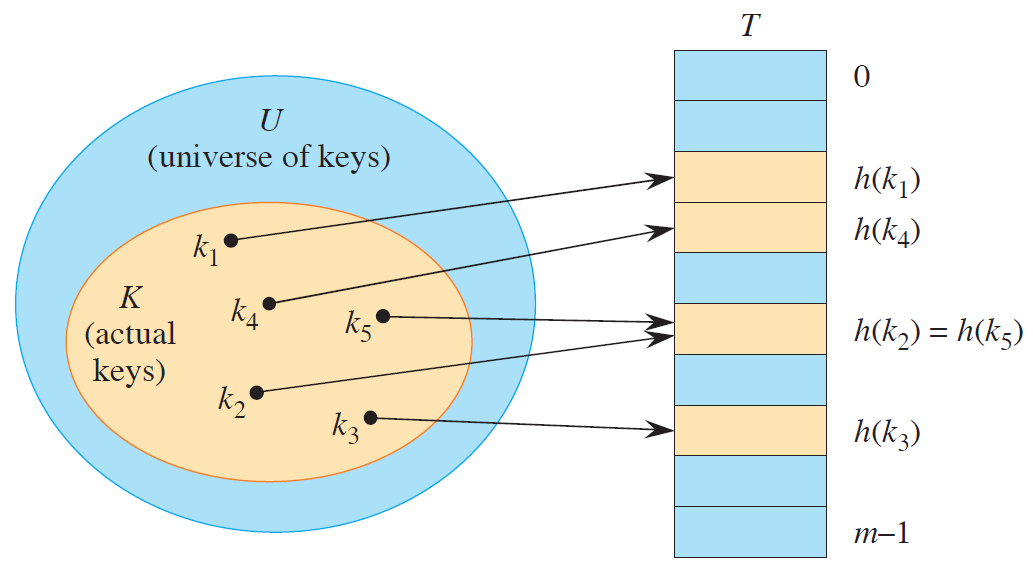
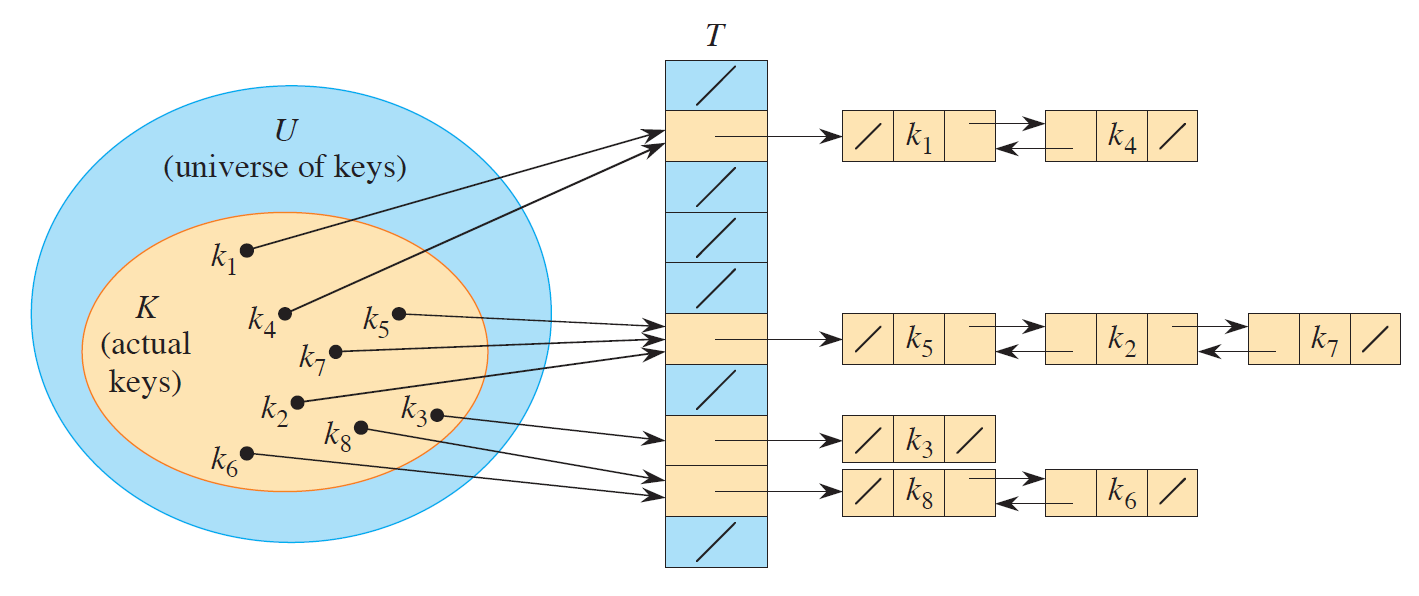
h : U → { 0 , 1 , . . . , m − 1 } h: U \rightarrow \{0,1,...,m - 1\} h : U → { 0 , 1 , ... , m − 1 }
定义
一个理想的哈希函数 h 有如下性质,对于每一个可能的输入 k,输出 h(k) 独立并随机从范围 {0,1,...,m-1} 中选择一个元素。一旦 h(k) 确定之后,之后对同一个元素 k 将产生相同的输出 h(k)
负载因子
给定一个哈希表 T,有 m 个插槽并储存 n 个元素,负载因子 α \alpha α
所有 n 个 key 都哈希到同一个插槽中,从而形成一个长度为 n 的链表,这时查找元素的最坏情况下的时间复杂度为 Θ ( n ) \Theta(n) Θ ( n )
假定使用均匀独立哈希函数 h,则任意两个不同的 k 1 k_1 k 1 k 2 k_2 k 2 1 / m 1 / m 1/ m j = 0 , 1 , . . . , m − 1 j=0,1,...,m-1 j = 0 , 1 , ... , m − 1 T [ j ] T[j] T [ j ] n j n_j n j n = n 0 + n 1 + ⋯ + n m − 1 n = n_0 + n_1 + \cdots + n_{m-1} n = n 0 + n 1 + ⋯ + n m − 1 E [ n j ] = α = n / m E[n_j] = \alpha = n/m E [ n j ] = α = n / m
定理
给定一个哈希表通过链接来解决冲突,并且假定使用均匀独立哈希函数,在平均情况下查找的时间复杂度为 Θ ( 1 + α ) \Theta(1 + \alpha) Θ ( 1 + α )
定义
对于任意数据都使用一个固定的哈希函数,其随机性仅仅来源于输入的分布(通常是未知的)
h ( k ) = k mod m h(k) = k \text{ mod } m h ( k ) = k mod m
h ( k ) = ⌊ m ( k A mod 1 ) ⌋ , 0 < A < 1 h(k) = \lfloor m(kA \text{ mod } 1)\rfloor,\quad 0 < A < 1 h ( k ) = ⌊ m ( k A mod 1 )⌋ , 0 < A < 1
其中 k A mod 1 kA \text{ mod } 1 k A mod 1 k A kA k A k A − ⌊ k A ⌋ kA - \lfloor kA \rfloor k A − ⌊ k A ⌋
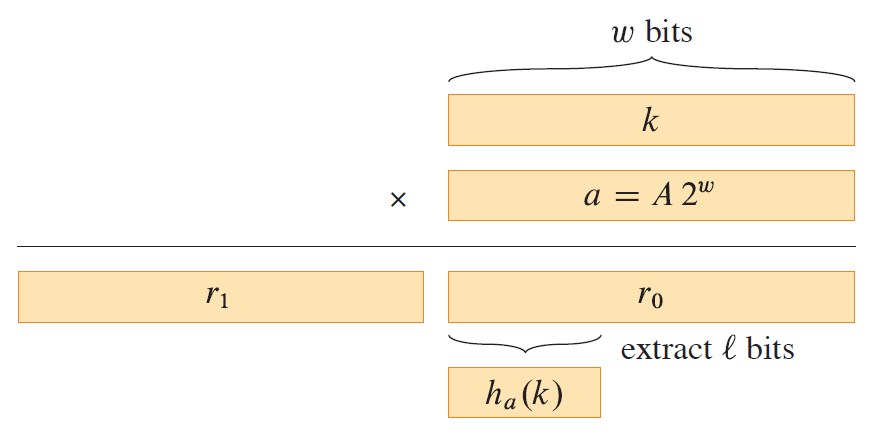
h a ( k ) = ( k a mod 2 w ) > > > ( w − l ) h_a(k) = (ka \text{ mod } 2^w) >>> (w - l) h a ( k ) = ( ka mod 2 w ) >>> ( w − l )
其中 m = 2 l m = 2^l m = 2 l l ≤ w l \le w l ≤ w
定义
设计一个合适的哈希函数集合,并在运行时随机从该集合中选择一个哈希函数,其随机性与输入无关;该方法的一个特例是统一哈希。
universal 哈希
令 H \mathcal{H} H k 1 k_1 k 1 k 2 k_2 k 2 h ( k 1 ) = h ( k 2 ) h(k_1) = h(k_2) h ( k 1 ) = h ( k 2 ) ∣ H ∣ / m |\mathcal{H}| / m ∣ H ∣/ m H \mathcal{H} H k 1 k_1 k 1 k 2 k_2 k 2 1 / m 1 / m 1/ m
H \mathcal{H} H k k k q q q h ( k ) = q h(k) = q h ( k ) = q 1 / m 1/m 1/ m H \mathcal{H} H k 1 k_1 k 1 k 2 k_2 k 2 h ( k 1 ) = h ( k 2 ) h(k_1) = h(k_2) h ( k 1 ) = h ( k 2 ) 1 / m 1/m 1/ m H \mathcal{H} H ϵ \epsilon ϵ k 1 k_1 k 1 k 2 k_2 k 2 h ( k 1 ) = h ( k 2 ) h(k_1) = h(k_2) h ( k 1 ) = h ( k 2 ) ϵ \epsilon ϵ 选择一个足够大的质数 p 使得 0 ≤ k ≤ p − 1 0 \le k \le p - 1 0 ≤ k ≤ p − 1 Z p \mathcal{Z}_p Z p { 0 , 1 , . . . , p − 1 } \{0,1,...,p-1\} { 0 , 1 , ... , p − 1 } Z p ∗ \mathcal{Z}_p^* Z p ∗ { 1 , 2 , . . . , p − 1 } \{1,2,...,p-1\} { 1 , 2 , ... , p − 1 } a ∈ Z p ∗ a \in \mathcal{Z}_p^* a ∈ Z p ∗ b ∈ Z p b \in \mathcal{Z}_p b ∈ Z p
h a b ( k ) = ( ( a k + b ) mod p ) mod m h_{ab}(k) = ((ak + b) \text{ mod } p) \text{ mod } m h ab ( k ) = (( ak + b ) mod p ) mod m
给定 p 和 m,所有这样的哈希函数集合是
H p m = { h a b : a ∈ Z p ∗ and b ∈ Z p } \mathcal{H}_{pm} = \{h_{ab} : a \in \mathcal{Z}_p^* \text{ and } b \in \mathcal{Z}_p\} H p m = { h ab : a ∈ Z p ∗ and b ∈ Z p }
定理
上述哈希函数集合 H p m \mathcal{H}_{pm} H p m
h ( k ) = S H A − 256 ( k ) mod m h(k) = SHA-256(k) \text{ mod } m h ( k ) = S H A − 256 ( k ) mod m
h a ( k ) = S H A − 256 ( a || k ) mod m h_a(k) = SHA-256(a \text{ || } k) \text{ mod } m h a ( k ) = S H A − 256 ( a || k ) mod m
h : U × { 0 , 1 , . . . , m − 1 } → { 0 , 1 , . . . , m − 1 } h: U \times \{0,1,...,m-1\} \rightarrow \{0,1,...,m-1\} h : U × { 0 , 1 , ... , m − 1 } → { 0 , 1 , ... , m − 1 }
HASH - INSERT (T,k) i = 0 repeat q = h (k,i) if T [q] == NIL T [q] = k return q else i = i + 1 until i == m error "hash table overflow" HASH - SEARCH (T,k) i = 0 repeat q = h (k,i) if T [q] == k return q i = i + 1 until T [q] == NIL or i == m return NIL h ( k , i ) = ( h 1 ( k ) + i h 2 ( k ) ) mod m h(k,i) = (h_1(k) + i h_2(k)) \text{ mod } m h ( k , i ) = ( h 1 ( k ) + i h 2 ( k )) mod m
h ( k , i ) = ( h 1 ( k ) + i ) mod m h(k,i) = (h_1(k) + i) \text{ mod } m h ( k , i ) = ( h 1 ( k ) + i ) mod m
相关信息
给定一个开放寻址的哈希表,负载因子 α = n / m < 1 \alpha = n/m < 1 α = n / m < 1 1 / ( 1 − α ) 1/(1-\alpha) 1/ ( 1 − α )
相关信息
给定一个开放寻址的哈希表,负载因子 α = n / m < 1 \alpha = n/m < 1 α = n / m < 1
1 α l n 1 1 − α \frac{1}{\alpha} ln \frac{1}{1-\alpha} α 1 l n 1 − α 1