提示
辐射度量学提供了一组思想和数学工具用来描述光的传播和反射,是渲染算法推导的基础。
Q=λhc
其中 c=299,472,458 m/s, h≈6.626x10−34 m2kg/s
提示
辐射通量,也称为功率,表示单位时间内通过某一表面或空间区域内的总能量
Φ=Δt→0limΔtΔQ=dtdQ
相反,给定通量作为时间函数,我们可以通过对时间积分来计算总能量
Q=∫t0t1Φ(t)dt
提示
给定一个有限区域 A,辐照度表示进入该区域的平均功率密度,辐射出射度表示离开该区域的平均功率密度
E=AΦ
更一般地,可以通过极限计算在某一点 p 处的辐照度或辐射出射度
E(p)=ΔA→0limΔAΔΦ(p)=dAdΦ(p)
给定辐照度我们也可以通过对面积积分来计算通量
Φ=∫AE(p)dA
提示
考虑一个无限小的光源,强度表示该光源发射功率的角密度
I=Δω→0limΔωΔΦ=dωdΦ
同样地,给定强度作为方向函数 I(ω),我们可以通过对方向积分来计算通量
Φ=∫ΩI(ω)dω
提示
这是最后也是最重要的概念,表示单位面积单位方向的平均功率
L(p,ω)=Δω→0limΔωΔEω(p)=dωdEω(p)
其中 Eω 表示垂直于 ω 方向的表面上的辐照度,根据通量可以定义为
L=dωdA⊥d2Φ
Lλ=Δλ→0limΔλΔL=dλdL
通过对波长积分可以计算出辐射量
L=∫λ0λ1Lλ(λ)dλ
提示
所有辐射测量(如通量、辐射度等)都有相应的光度测量。光度测定是从人类视觉系统感知的角度研究可见电磁辐射。每个光谱辐射量都可以通过与光谱响应曲线积分转换为其相应的光度量,该曲线描述了人眼对各种波长的相对敏感度。
提示
亮度衡量光谱功率分布在人类观察者眼中的亮度,定义为
Y=∫λLλ(λ)V(λ)dλ
所有其他的辐射度量都有对应的光度测量
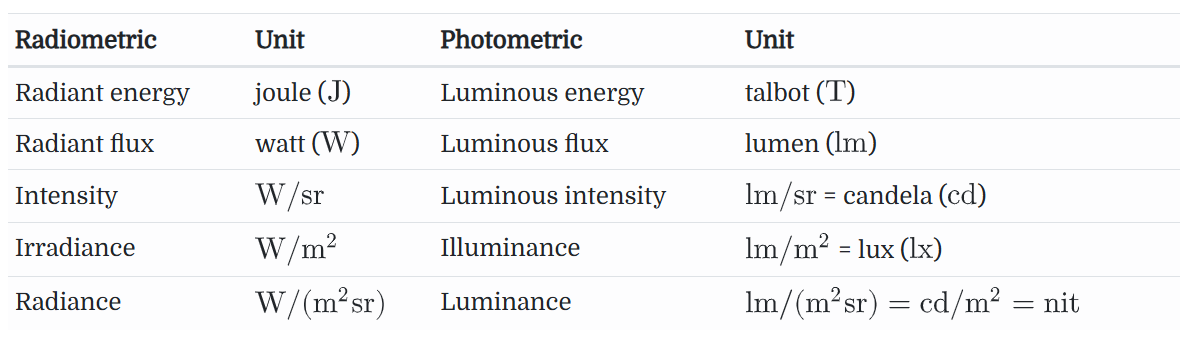
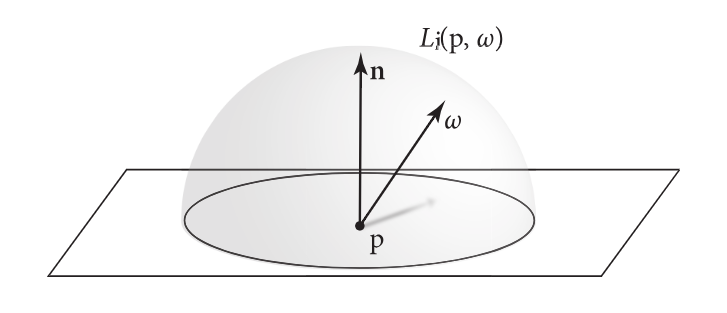
E(p,n)=∫ΩLi(p,ω)∣cosθ∣dω
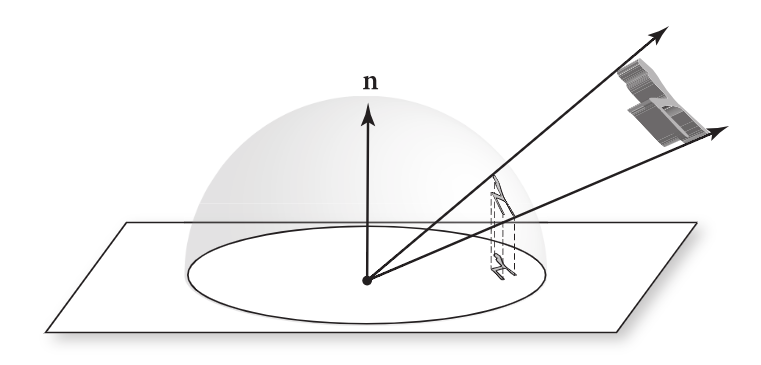
dω⊥=∣cosθ∣dω
则有
E(p,n)=∫H2(n)Li(p,ω)dω⊥
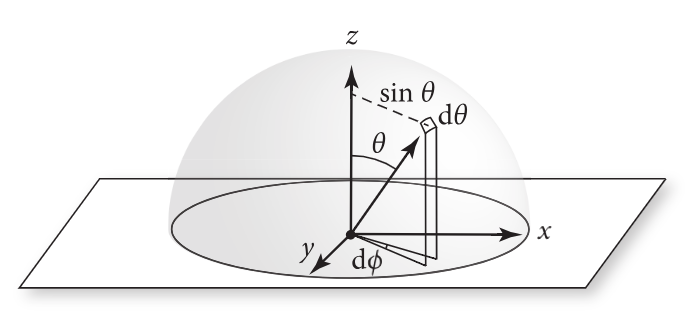
dω=sinθdθdϕ
则有
E(p,n)=∫02π∫0π/2Li(p,θ,ϕ)cosθsinθdθdϕ
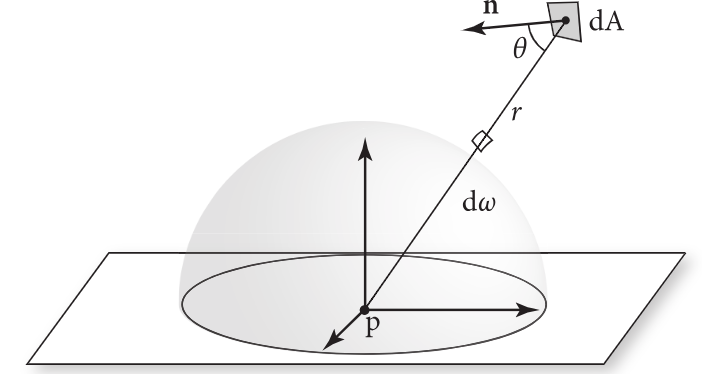
dω=r2dAcosθ
则有
E(p,n)=∫ALcosθir2cosθodA
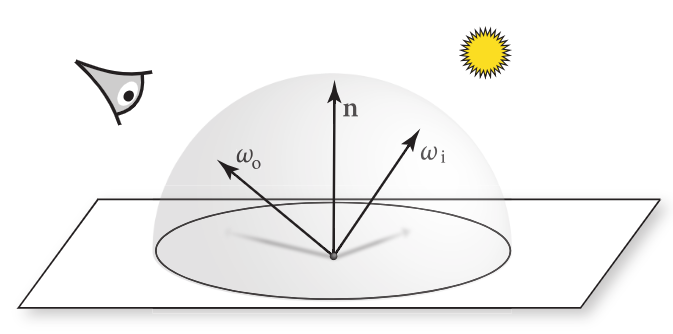
双向反射分布函数 BRDF 给出了描述表面反射的形式,给定入射方向 ωi,则点 p 处的微分辐照度为
dE(p,ωi)=Li(p,ωi)cosθidωi
一部分 radiance 将沿着方向 ωo 反射出去,又因为几何光学的线性假设,被反射的辐射度和入射的辐照度成正比
dLo(p,ωo)∝dE(p,ωi)
这个比例常数定义了表面的 BDDF fr
fr(p,ωo,ωi)=dE(p,ωi)dLo(p,ωo)=Li(p,ωi)cosθidωidLo(p,ωo)
提示
基于物理的 BRDF 具有两个重要性质:
- fr(p,ωi,ωo)=fr(p,ωo,ωi)
- 能量守恒:
∫H2(n)fr(p,ωo,ω′)cosθ′dω′≤1
半球定向反射
描述了表面上某一点收到来自半球方向的常量光照后,反射到给定方向上的比例,定义为
ρhd(ωo)=∫H2(n)fr(p,ωo,ωi)∣cosθi∣dωi
双向透射分布函数 BTDF ft 描述了透射光的分布,定义和 BRDF 类似,BRDF 和 BTDF 可以统一定义为双向散射分布函数 BSDF f
散射方程
Lo(p,ωo)=∫S2f(p,ωo,ωi)Li(p,ωi)∣cosθi∣dωi
反射方程
Lo(p,ωo)=∫H2(n)f(p,ωo,ωi)Li(p,ωi)∣cosθi∣dωi
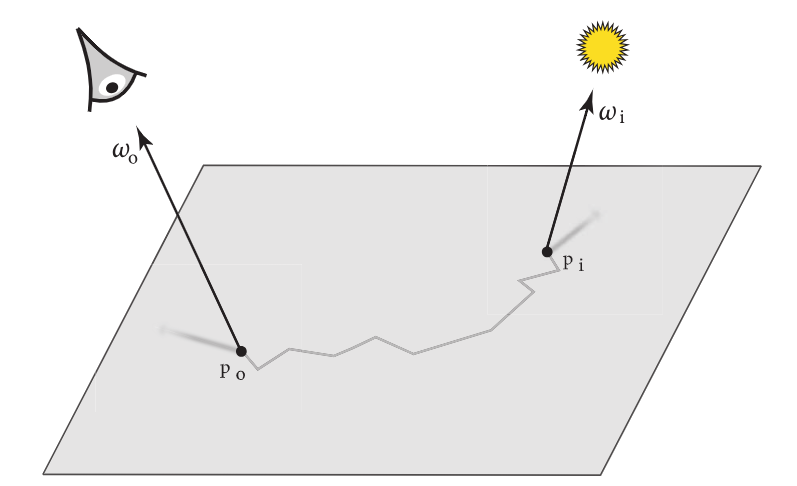
双向散射表面反射分布函数 BSSRDF 描述了经过次表面后的散射,定义为
S(po,ωo,pi,ωi)=dΦ(pi,ωi)dLo(po,ωo)
一般形式的散射方程
Lo(po,ωo)=∫A∫H(n)S(po,ωo,pi,ωi)Li(pi,ωi)∣cosθi∣dωidA






