堆排序

被子2024年9月2日大约 2 分钟

堆

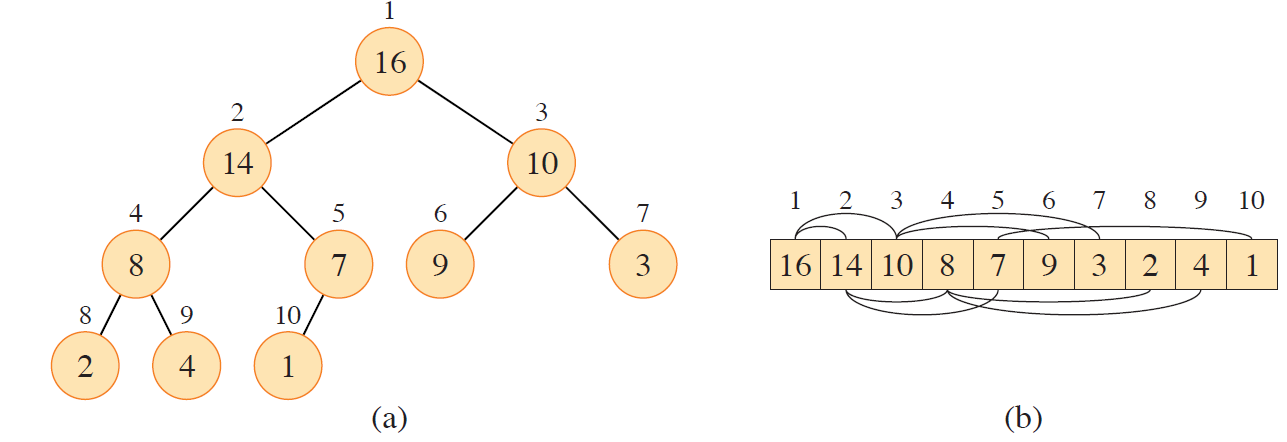
PARENT(i)
  return i/2
LEFT(i)
  return 2i
RIGHT(i)
  return 2i+1

维持堆的性质

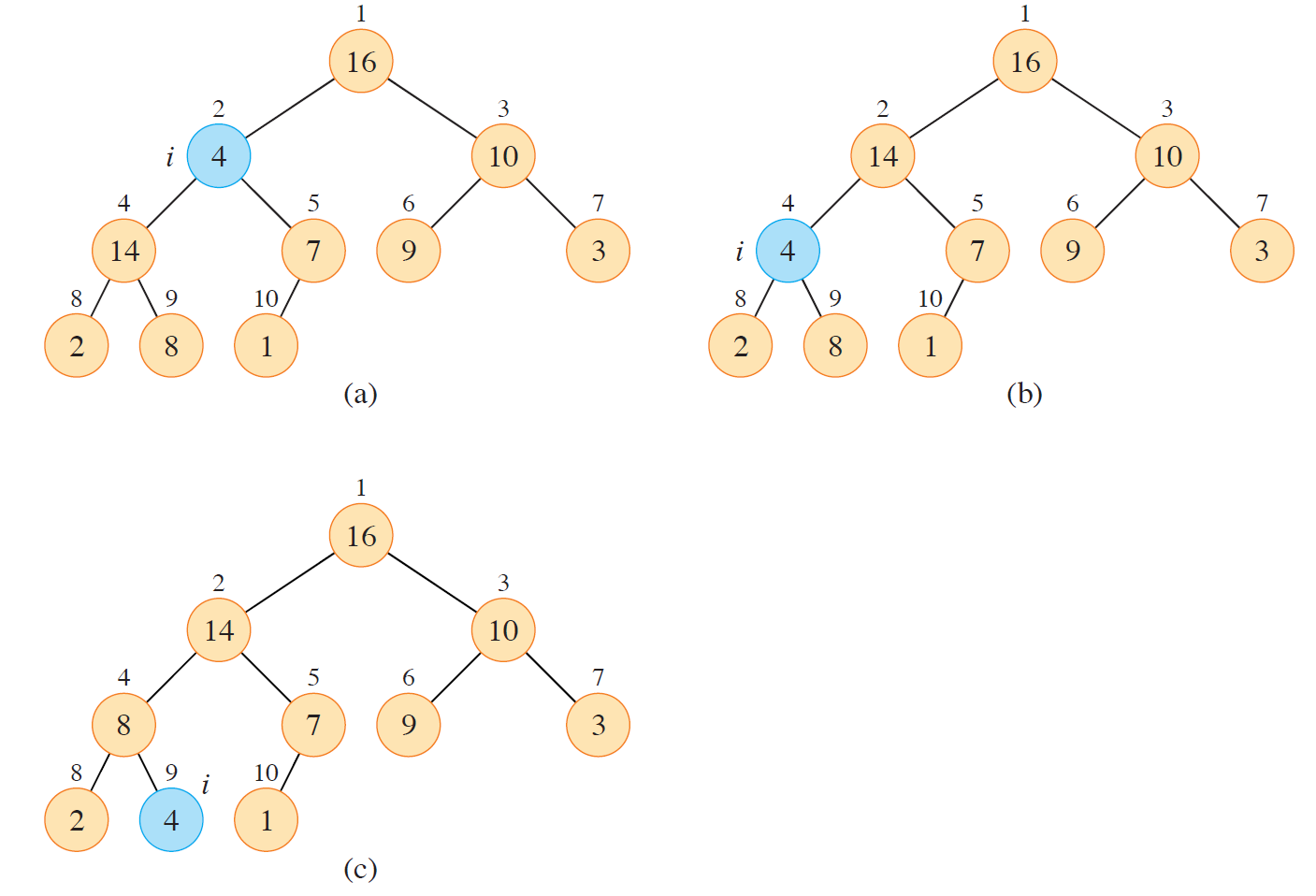
max_heapify(A,i)
  l = LEFT(i)
  r = RIGHT(i)
  if l ≤ A.heap-size and A[l] > A[i]
    largest = l
  else largest = i
  if r ≤ A.heap-size and A[r] > A[largest]
    largest = r
  if largest ≠ i
    exchange A[i] with A[largest]
    max_heapify(A,largest)

时间复杂度为 T(n) ≤ T(2n/3)+Θ(1) 根据主方法定理第二种情况可得 T(n) = O(lgn)

构造堆

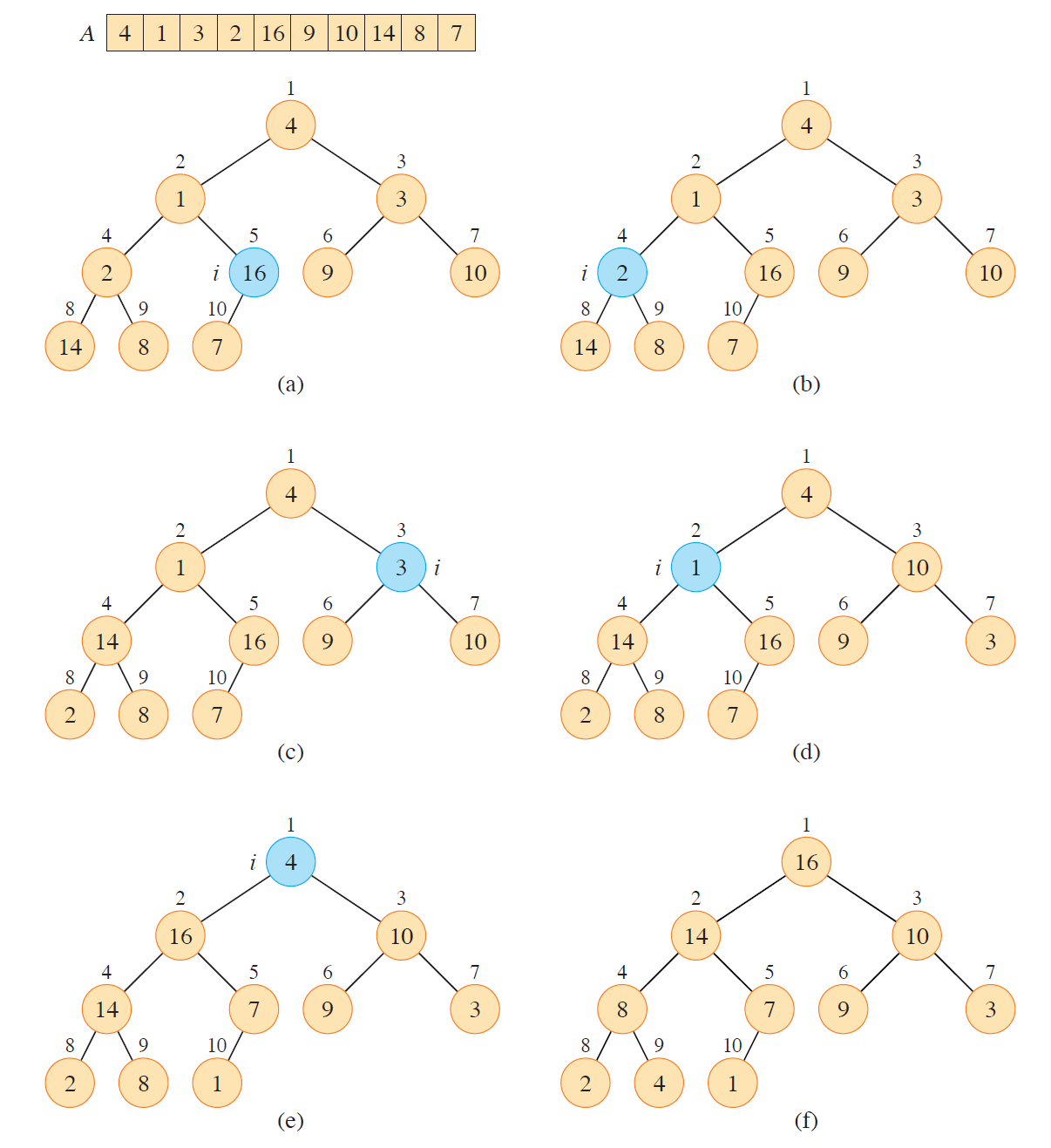
build_max_heap(A,n)
  A.heap-size = n
  for i = n/2 downto 1
    max_heapify(A,i)

时间复杂度

含有 n 个元素的堆的高度 $\lfloor n/2\rfloor$ ，并且在任一高度 h 最多有 $\lceil n/2^{h+1}\rceil$ 个结点，则有

\begin{aligned} T(n) &= \sum_{h=0}^{\lfloor lg\,n \rfloor} \left\lceil\frac{n}{2^{h+1}}\right\rceil ch \\[3px] &\le \sum_{h=0}^{\lfloor lg\,n \rfloor}\frac{n}{2^h}ch \\[3px] &= cn\sum_{h=0}^{\lfloor lg\,n \rfloor}\frac{h}{2^h} \\[3px] &\le cn\sum_{h=0}^{\infty}\frac{h}{2^h} \\[3px] &\le cn\cdot\frac{1/2}{(1-1/2)^2} \\[3px] &=\mathcal{O}(n) \end{aligned}

堆排序

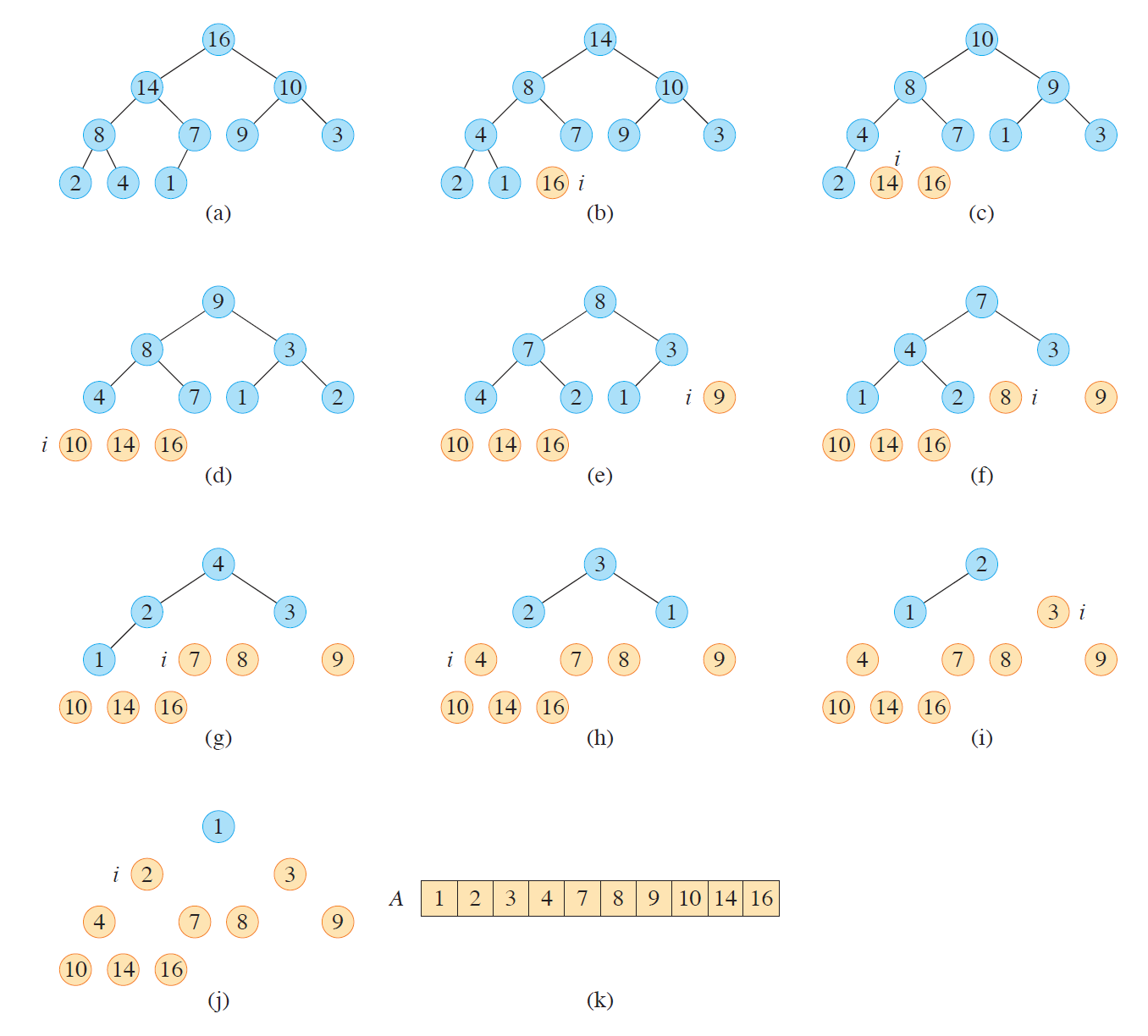
heapsort(A,n)
  build_max_heap(A,n)
  for i = n downto 2
    exchange A[1] with A[i]
    A.heap-size = A.heap-size - 1
    max_heapify(A,1)

时间复杂度为 O(nlgn)

优先级队列

max_heap_maximum(A)
  if A.heap-size < 1
    return "heap underflow"
  return A[1]

max_heap_extract_max(A)
  max = max_heap_maximum(A)
  A[1] = A[A.heap-size]
  A.heap-size = A.heap-size - 1
  max_heapify(A,1)
  return max

max_heap_increase_key(A,x,k)
  if k < x.key
    error "new key is smaller than current key"
  x.key = k
  // find the index i where A[i] = x
  while i > 1 and A[PARENT(i)].key < A[i].key
    exchange A[i] with A[PARENT(i)]
    i = PARENT(i)

max_heap_insert(A,x,n)
  if A.heap-size == n
    error "heap overflow"
  A.heap-size = A.heap-size + 1
  k = x.key
  x.key = -∞
  A[A.heap-size] = x
  max_heap_increase_key(A,x,k)