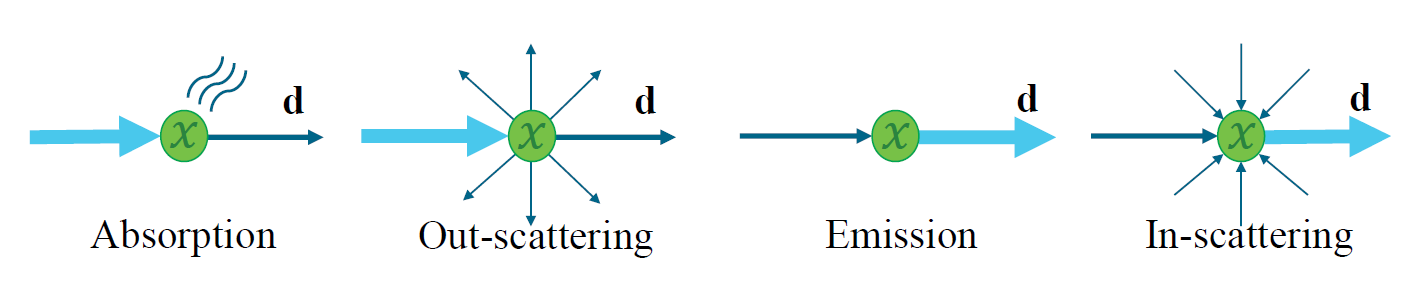

媒介的反射率 ρ 定义为:
ρ=σs+σaσs=σtσs
在参与介质的影响下,光在传播过程中的辐射度不再保持不变,某点的入射辐射度可以根据以下等式描述为(假设光源是无穷小的点光源):
Li(c,−v)=Tr(c,p)Lo(p,v)+∫t=0∥p−c∥Tr(c,c−vt)Lscat(c−vt,v)σsdt
透射率 Tr 表示有多少比例的光能够穿过一定距离的参与介质,根据 Beer-Lambert 定律可以表示为
Tr(xa,xb)=e−τ,whereτ=∫x=xaxbσt(x)∥dx∥
Lscat(x,v)=πi=1∑np(v,lci)v(x,plighti)clighti(∥x−plighti∥)
其中
p 表示相位函数
v 表示可见性函数
lci 表示到第 i 个点光源的方向
plighti 表示第 i 个点光源的位置
clighti 表示第 i 个点光源的辐射度
可见性函数 v(x,plighti) 表示有多少光可以从点光源 plighti 到达点 x 处,可以表示为
v(x,plighti)=shadowMap(x,plighti)⋅volShad(x,plighti)
其中
shadowMap 表示来自不透明对象的遮挡,volShad 表示在 volume 中的透射率
提示
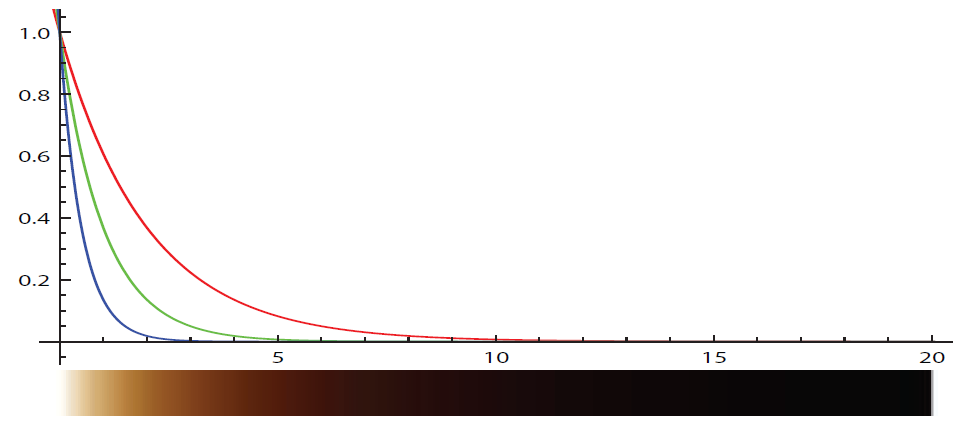
考虑 σs=(0.5,1,2) 和 σa=(0,0,0),当在介质中传播距离较短时,透射率 Tr≈1,此时散射事件将占据主导,材质将显示为蓝色;而当光越深入介质越少的光子可以通过,此时透射颜色将占据主导,材质将显示为红色。
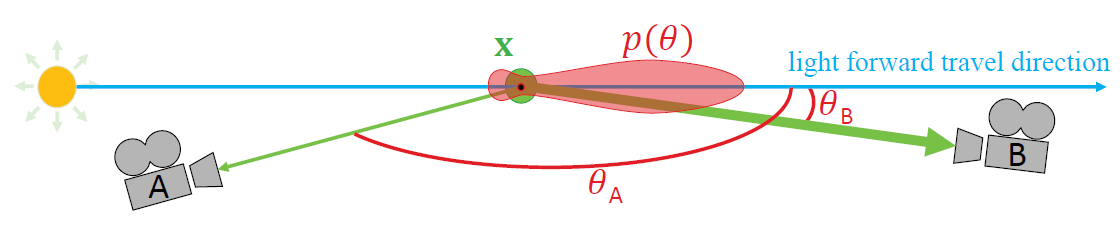 如图所示,相位函数在宏观层面上描述了散射方向的概率和分布,根据能量守恒原则,相位函数在单位球面上的积分必须等于 1;下面是最简单的相位函数,该函数是各向同性的,其在所有方向上均匀散射
如图所示,相位函数在宏观层面上描述了散射方向的概率和分布,根据能量守恒原则,相位函数在单位球面上的积分必须等于 1;下面是最简单的相位函数,该函数是各向同性的,其在所有方向上均匀散射
p(θ)=4π1
基于物理的相位函数依赖于粒子的相对大小 sp
sp=λ2πr
其中 r 表示粒子半径,λ 表示所考虑的光的波长
提示
当 sp≪1 时,会发生 Rayleigh 散射(例如空气)
Rayleigh 散射的相位函数在极坐标下的图示如下,相对于光的方向有前向散射和后向散射两个部分
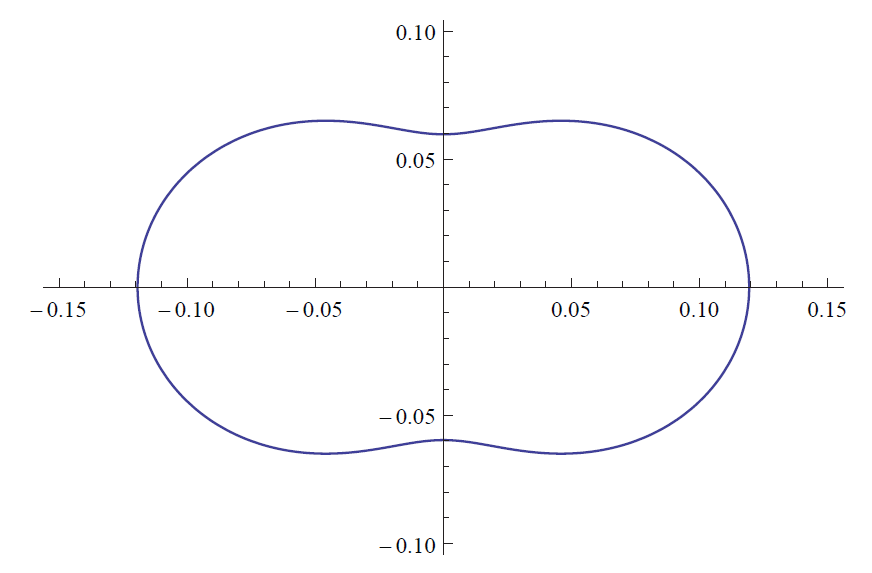
具体可以表示为
p(θ)=16π3(1+cos2θ)
Rayleigh 散射具有强烈的波长依赖性,当作为波长 λ 的函数来看时,其散射系数 σs 与波长的四次方倒数成正比
σs(λ)∝λ41
这意味着短波长的蓝光或紫光比长波长的红光散射得更多,其光谱分布可以通过光谱的颜色匹配函数转换为 RGB 值 σs=(0.490,1.017,2.339),该值被归一化为 1 的亮度,应该根据所需要的散射强度进行缩放。
提示
当 sp≈1 时,会发生 Mie 散射
Mie 散射的相位函数通常是一种复杂的分布,对于特定的粒子大小来说,具有强烈而尖锐的方向性;而介质中的粒子尺寸一般具有连续的分布,对这些不同尺寸下的相位函数进行平均可以得到一个更平滑的相位函数,因此相对平滑的相位函数可以被用来表示 Mie 散射。
一种常用的相位函数是 Henyey-Greenstein (HG),该函数可以很好地匹配朝向主要散射方向的部分,可以被用于表示烟、雾、尘埃等介质。这种介质可以表现出强烈的后向或前向散射,从而在光源周围产生较大的视觉光晕,例如雾气中的聚光灯以及太阳方向云层边缘强烈的银边效应。
HG 相位函数表示为
phg(θ,g)=4π(1+g2−2gcosθ)1.51−g2,g∈[−1,1]
g < 0 表示后向散射,g = 0 表示各向同性,g > 0 表示前向散射
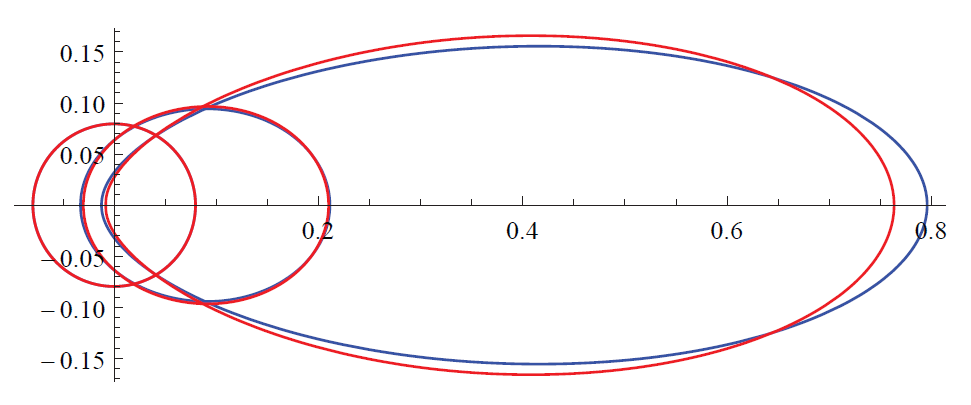
Schlick 相位函数是比 HG 更快的一个近似函数,表示为
p(θ,k)=4π(1+kcosθ)21−k2,k≈1.55g−0.55g3
提示
当 sp≫1 时,会发生几何散射
几何散射发生在粒子尺寸明显大于光的波长的情况下,此时,光可以在每个粒子内部发生折射和反射,在宏观层面上需要一个复杂的散射相位函数来模拟;光的偏振也会影响这种类型的散射,例如现实生活中的视觉彩虹效应,这种效应是由空气中水滴内部对光的反射引起的,它将太阳光分散成可见光谱,并在小角度的后向散射范围内形成可见的彩虹。
参考
Display of The Earth Taking into Account Atmospheric Scattering
Allan Zucconi: Volumetric Atmospheric Scattering

T(CP)=ICIP

IPA=IPS(λ,θ,h)T(PA)=ICT(CP)S(λ,θ,h)T(PA)=in−scatteringICS(λ,θ,h)out−scatteringT(CP)T(PA)

IA=P∈AB∑IPAds=P∈AB∑ICS(λ,θ,h)T(CP)T(PA)ds=ISP∈AB∑S(λ,θ,h)T(CP)T(PA)ds
S(λ,θ,h)=2π2(n2−1)2densityNρ(h)λ41wavelengthgeometry1+cos2θ
其中:
- λ: 入射光的波长
- θ: 散射角度
- h: 海拔高度
- n=1.00029:空气的折射率
- N=2.504⋅1025:标准大气压下的分子数量密度
- ρ(h):密度比,在海平面处等于 1
βR(λ,h)=38π3(n2−1)2Nρ(h)λ41
数学推导
βR(λ,h)=∫02π∫0πS(λ,θ,h)sinθdθdϕ=∫02π∫0πconstant2π2(n2−1)2Nρ(h)λ41(1+cos2θ)sinθdθdϕ=2π2(n2−1)2Nρ(h)λ41∫02π∫0π(1+cos2θ)sinθdθdϕ=2π2(n2−1)2Nρ(h)λ41∫02π38dϕ=38π3(n2−1)2Nρ(h)λ41
βR(λ)=βR(λ,0)βR(680nm)βR(550nm)βR(440nm)=38π3(n2−1)2N1λ41=0.00000519673=0.0000121427=0.0000296453
原始的 Rayleigh 散射函数可以分解成两部分,一个表示 Rayleigh 散射系数,另一个表示 Rayleigh 相位函数:
SR(λ,θ,h)=βR(λ,h)γR(θ)
则
γR(θ)=β(γ)S(λ,θ,h)=S(λ,θ,h)2π2(n2−1)2Nρ(h)λ41(1+cos2θ)β(λ)18π3(n2−1)23ρ(h)Nλ4=16π3(1+cos2θ)
ρ(h)=density(0)density(h)=exp{−H0h}
对于 Rayleigh 散射,H0=8500 m;对于 Mie 散射, H0=1200 m

IP=IQexp{−β(λ,h1)QP}=ISexp{−β(λ,h0)CQ}exp{−β(λ,h1)QP}=ISexp{−β(λ,h0)CQ−β(λ,h1)QP}
如果 CQ=QP,则
IP=ISexp{−(β(λ,h0)+β(λ,h1))ds}=ISexp{−Q∈CP∑β(λ,hQ)ds}
由此可得,
T(CP)=ISIP=exp{−Q∈CP∑β(λ,hQ)ds}=exp{−Q∈CP∑β(λ,0)ρ(hQ)ds}=exp{−β(λ,0)Q∈CP∑ρ(hQ)dsoptical depth D(CP)}=exp{−β(λ)D(CP)}
βM(h)=38π3(n2−1)2Nρ(h)
γM(θ,g)=4π1(1+g2−2gcosθ)3/21−g2
γM(θ,g)=8π32+g21−g2(1+g2−2gcosθ)3/21+cos2θ
γM(θ,g)=4π1(1+gcosθ)21−g2




 如图所示,相位函数在宏观层面上描述了散射方向的概率和分布,根据能量守恒原则,相位函数在单位球面上的积分必须等于 1;下面是最简单的相位函数,该函数是各向同性的,其在所有方向上均匀散射
如图所示,相位函数在宏观层面上描述了散射方向的概率和分布,根据能量守恒原则,相位函数在单位球面上的积分必须等于 1;下面是最简单的相位函数,该函数是各向同性的,其在所有方向上均匀散射




