当函数的球谐投影绕某一个轴旋转对称时被称为 Zonal Harmonics，若这一个轴是 z 轴，则函数值等于 0 的部分会形成相同维度上的线且该函数只依赖于 $\theta$ 。此时该方向的投影在每一个 band 上只有一个非零系数。ZH 旋转比一般的 SH 更简单，给定一个函数的 ZH 系数 $z_l$ （ SH 投影中 m = 0 部分），可以使用以下公式将其旋转到新的方向 $d$ 上

f(s) = \sum_l z_l\sqrt{\frac{4\pi}{2l+1}}\sum_z y_l^m(d)\,y_l^m(s)

对应的 SH 系数是

f_l^m = \sqrt{\frac{4\pi}{2l+1}}z_l\,y_l^m(d)

SH 乘积

使用 $n^{th}$ 重构表示的两个函数 $f$ 和 $g$ 的乘积投影后的 $k^{th}$ 系数等于

p_k = \int y_k(s)\left(\sum_{i=0}^{n^2}f_i\,y_i(s)\right)\left(\sum_{j=0}^{n^2}g_j\,y_j(s)\right)ds = \sum_{ij}\Gamma_{ijk}f_i\,g_j

其中

\Gamma_{ijk} = \int y_i(s)\,y_j(s)\,y_k(s)\,ds

环境映射

定义

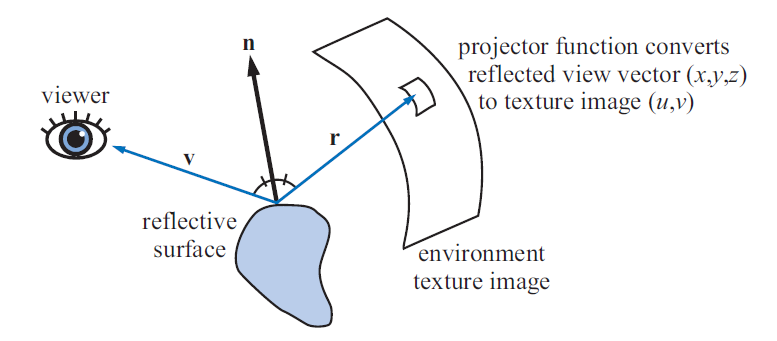
环境映射将一个球面函数记录到一个或多个纹理中，可以表达任意高频率的球面信号（通过提高纹理分辨率）以及精确捕捉任意范围的环境辐射度（通过提高每个通道的位数）

反射映射是其中最基本的一种，其假定 BRDF 是一个完美的镜面，反射方程可以简化为

L_o(v) = F(n,r)L_i(r)

由于输入辐射度 $L_i$ 只依赖于方向，因此可以存到一个二维表格中（即环境贴图），反射映射的算法具体步骤如下

生成环境贴图
对于每一个像素，计算物体表面该位置处的法线
根据观察方向 $v$ 和法线 $n$ 计算对应的反射方向 $r$
根据反射方向 $r$ 计算对应环境贴图中的索引，从而得到输入辐射度

注意

环境映射不适用于平面的情况

有很多投影函数可以将反射向量 $r$ 映射到环境贴图中

纬度-经度映射

给定归一化的反射向量 $r=(r_x,r_y,r_z)$ ，可以计算出球面坐标 $(\rho,\phi)$ ， $\phi \in [0,2\pi)$ 表示经度， $\rho \in [0,\pi]$ 表示纬度

\begin{aligned} \rho &= arccos(r_z) \\ \phi &= atan2(r_y,r_x) \end{aligned}

球面映射

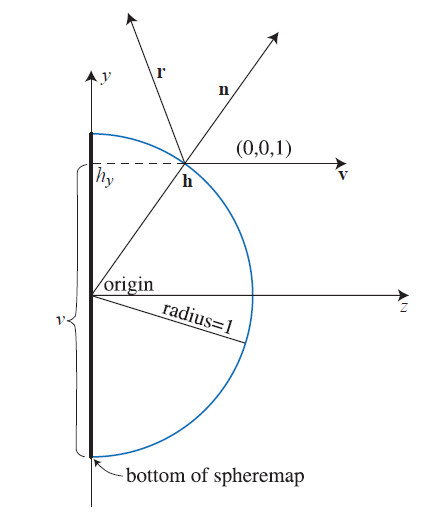
球面映射将反射向量投影到球面的二维贴图上（即球面贴图），具体计算步骤如下：

根据反射向量 $r$ 和观察方向 $v$ 计算出对应的球面法线 $n$ , 在球面空间中 $v$ 固定等于 $(0,0,1)$ ，则
$n = \frac{r + v}{\|r+v\|} = \left(\frac{r_x}{m}, \frac{r_y}{m}, \frac{r_z+1}{m}\right),\quad m = \sqrt{r_x^2+r_y^2+(r_z+1)^2}$
假设球在原点且半径等于 1，则该法线的坐标也是球面上该点 $h$ 的坐标，则 $(h_x,h_y)$ 表示了球面贴图上的一点，范围是 $[-1,1]$ ，将其映射到范围 $[0,1]$ 可得
$\begin{aligned} u &= \frac{r_x}{2m} + 0.5 \\ v &= \frac{r_y}{2m} + 0.5 \end{aligned}$

注意

球面贴图是从一个固定的方向来获取整个环境的视图，虽然也可以从新的观察方向来计算出对应的纹理坐标，然而这么做会产生视觉瑕疵，这是因为原球面贴图中的小部分在新的观察方向下被放大了。

立方体映射

可以直接使用反射向量 $r=(r_x,r_y,r_z)$ 作为纹理坐标进行访问

IBL

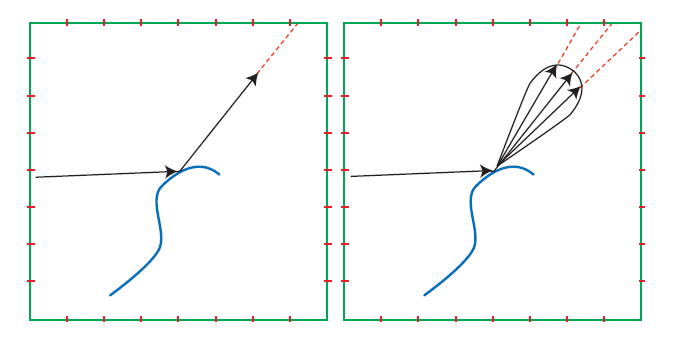
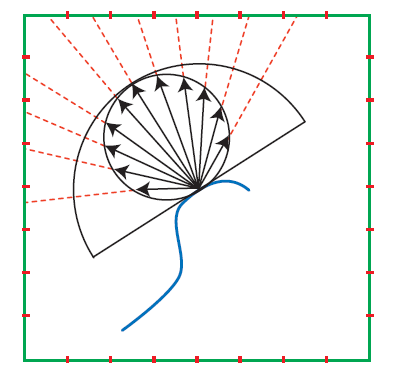
当使用环境贴图来表示环境光时，需要使用渲染方程积分来计算光照信息，可以用蒙特卡洛估计

\int_H L_i(l)\,f(l,v)\,cos\theta_l\,dl \approx \frac{1}{N}\sum_{k=1}^N \frac{L_i(l_k)\,f(l_k,v)\,cos\theta_{l_k}}{p(l_k,v)}

即使使用重要性采样，该方法仍然需要很多次采样计算，为了进一步减少计算代价，可以使用 Split Sum 近似

Sepcular IBL

如果 BRDF 是 glossy 的，此时满足条件积分域 $\Omega_G$ 足够小，则有

\int_H L_i(l)\,f(l,v)\,cos\theta_l\,dl \approx \underbrace{\frac{\int_{H}L_i(l)\,dl}{dl}}_{对环境贴图作\, prefilter} \underbrace{\int_H f(l,v)\,cos\theta_l\,dl}_{预计算 \,LUT}

\begin{aligned} \int_H f(l,v)\,cos\theta_l\,dl &= F_0\int_H\frac{f(l,v)}{F(v,h)}\Big(1 - (1 - v\cdot h)^5\Big)\,cos\theta_l\,dl + \int_H \frac{f(l,v)}{F(v,h)}(1-v\cdot h)^5\,cos\theta_l\,dl \\ & \approx F_0\,\Big(\frac{1}{N}\sum_{k=1}^N \frac{D(h_k)\cdot G(l_k,v)\cdot (1 - (1 - v\cdot h)^5)\,|n\cdot l|}{4|n\cdot l||n\cdot v|\,p(l_k,v)}\Big) + \frac{1}{N}\sum_{k=1}^N \frac{D(h_k)\cdot G(l_k,v)\cdot (1 - v\cdot h)^5\,|n\cdot l|}{4|n\cdot l||n\cdot v|\,p(l_k,v)} \end{aligned}

1. Prefilter

在 Real Shading in Unreal Engine 4 中，使用 GGX 重要性采样来进行蒙特卡洛估计，并且使用 $n\cdot l$ 做加权平均，即

\frac{\int_H L_i(l)\,dl}{dl} \approx \frac{1}{\sum_{k=1}^N |n\cdot l_k|} \sum_{k=1}^N L_i(l_k)\,|n\cdot l_k|

警告

由于 GGX 采样分布依赖于观察方向，而此处默认使用 $n = v = r$ 的观察方向来进行采样，因此导致在 grazing angle 处得到的反射不够充分

2. BRDF LUT

同样使用重要性采样 $D(h)|n\cdot h|$ ，这是因为

\int_\Omega D(h)|n\cdot h|\,dh = 1

又我们要对 $l$ 进行采样而不是 $h$ ，因此需要使用 Jacobian 变换

J(h) = \frac{1}{4|v\cdot h|}

可得

pdf(l_k,v) = \frac{D(h)|n\cdot h|}{4|v\cdot h|}

综上

提示

\int_H f(l,v)\,cos\theta_l\,dl \approx F_0\,\Big(\frac{1}{N}\sum_{k=1}^N \frac{G(l_k,v)\cdot|v\cdot h|\cdot (1 - (1 - v\cdot h)^5)}{|n\cdot h||n\cdot v|}\Big) + \frac{1}{N}\sum_{k=1}^N\frac{G(l_k,v)\cdot|v\cdot h|\cdot(1-v\cdot h)^5}{|n\cdot h||n\cdot v|}

Diffuse IBL

1. Irradiance environment map

\begin{aligned} L_o(p,\omega_o) &= k_d\frac{c}{\pi}\int_{\Omega} L_i(p,\omega_i)\,|n\cdot \omega_i|\,d\omega_i \\ L_o(p,\phi_o,\theta_o) &= k_d\frac{c}{\pi}\int_{\phi=0}^{2\pi}\int_{\theta=0}^{\frac{1}{2}\pi} L_i(p,\phi_i,\theta_i)\,cos\theta\,sin\theta\,d\phi\,d\theta \end{aligned}

使用黎曼和近似估计，将 $\phi$ 划分成 $n_1$ 份，将 $\theta$ 划分成 $n_2$ 份，则

\begin{aligned} L_o(p,\phi_o,\theta_o) &\approx k_d\frac{c}{\pi} \sum_{\phi=0}^{n_1}\sum_{\theta=0}^{n_2} \frac{2\pi}{n_1}\frac{\frac{1}{2}\pi}{n_2} L_i(p,\phi_i,\theta_i)\,cos\theta\,sin\theta \\ &= k_d\frac{c\pi}{n_1n_2} \sum_{\phi=0}^{n_1}\sum_{\theta=0}^{n_2} L_i(p,\phi_i,\theta_i)\,cos\theta\,sin\theta \end{aligned}

2. Spherical harmonics

球谐系数 $Y_{lm}$ 中的前 9 个可以预先计算得到，具体如下

\begin{aligned} (x,y,z) \quad &= \quad (sin\theta\,cos\phi,sin\theta\,sin\phi,cos\theta) \\ Y_{00}(\theta,\phi) \quad &= \quad 0.282095 \\ (Y_{11};Y_{10};Y_{1-1})(\theta,\phi) \quad &= \quad 0.488603(x;z;y) \\ (Y_{21};Y_{2-1};Y_{2-2})(\theta,\phi) \quad &= \quad 1.092548(xz;yz;xy) \\ Y_{20}(\theta,\phi) \quad &= \quad 0.315392(3z^2-1) \\ Y_{22}(\theta,\phi) \quad &= \quad 0.546274(x^2-y^2) \end{aligned}

又

E(n) = \int_{\Omega(n)} L(\omega)\,(n\cdot \omega)\,d\omega

其中 $E$ 和 $L$ 可以通过球谐函数系数来表示

\begin{aligned} L(\theta,\phi) &= \sum_{l,m} L_{lm}Y_{lm}(\theta,\phi) \\ E(\theta,\phi) &= \sum_{l,m} E_{lm}Y_{lm}(\theta,\phi) \end{aligned}

我们定义 $A=(n\cdot\omega)$ ，由于 $A$ 没有方位角 $\phi$ 依赖， $m=0$ 因此我们可以只使用 $l$ 索引

A(\theta) = max[cos\theta,0] = \sum_l A_lY_{l0}(\theta)

可以证明

E_{lm} = \sqrt{\frac{4\pi}{2l+1}} A_lL_{lm}

为了方便，我们定义一个新的变量

\hat{A_l} = \sqrt{\frac{4\pi}{2l+1}}A_l

综上

提示

E(\theta,\phi) = \sum_{l,m} \hat{A_l} L_{lm}Y_{lm}(\theta,\phi)